基本思想
分而治之方法與軟體設計的模組化方法非常相似。為了解決一個大的問題,可以:
1) 把它分成兩個或多個更小的問題;
2) 分別解決每個小問題;
3) 把各小問題的解答組合起來,即可得到原問題的解答。小問題通常與原問題相似,可以遞歸地使用分而治之策略來解決。分而治之方法可以用於實現不同的排序方法,這裡介紹兩種排序法:快速排序(quick sort)和歸併排序 。
解決排序問題
算法思想
在快速排序中,n 個元素被分成三段(組):左段left,右段right 和中段middle。中段僅包含一個元素。左段中各元素都小於等於中段元素,右段中各元素都大於等於中段元素。因此left 和right 中的元素可以獨立排序,並且不必對left 和right 的排序結果進行合併。middle 中的元素被稱為支點( pivot )。下面給出快速排序的偽代碼。
使用快速排序方法對a [ 0 : n- 1 ] 排序。
從a [ 0 : n- 1 ] 中選擇一個元素作為middle,該元素為支點把餘下的元素分割為兩段left 和right,使得left中的元素都小於等於支點,而right 中的元素都大於等於支點。
遞歸地使用快速排序方法對left 進行排序。
遞歸地使用快速排序方法對right 進行排序。
所得結果為left + middle + right。
考察元素序列[ 4 , 8 , 3 , 7 , 1 , 5 , 6 , 2 ]。
假設選擇元素6 作為支點,則6 位於middle;4,3,1,5,2 位於l e f t;8,7 位於right。當left 排好序後,所得結果為1,2,3,4,5;當right 排好序後,所得結果為7,8。把right 中的元素放在支點元素之後,left 中的元素放在支點元素之前,即可得到最終的結果[ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 ] 。
快速排序算法
把元素序列劃分為left、middle 和right 可以就地進行。在程式1 中,支點總是取位置1 中的元素。也可以採用其他選擇方式來提高排序性能。
程式1:快速排序
#define MAXSIZE 20
typedef int KeyType;
typedef struct {
KeyType key;
InfoType otherinfo;
} RedType;
typedef struct {
RedType r [MAXSIZE+1];
int length;
} SqList;
int Partition (SqList &L, int low, int high) {
L.r [0] =L.r [low];
Pivotkey=L.r [low] .key;
While (low<high) {
While (low<high&&L.r [high] .key>=pivotkey)
--high;
L.r [low] =L.r [high];
While (low<high&&L.r [low] .key<=pivotkey) +
+low;
L.r [high] =L.r [low];
}
L.r [low] =L.r [0];
Return low;
}
void Qsort (SqList &L, int low, int high) {
if (low<high) {
pivotloc=Partition (L, low, high);
QSort (L, low, pivotloc-1);
Qsort (L, pivotloc+1, high);
}
}
void QuickSort (SqList &L) {
Qsort (L, 1, L.length);
}
求順序統計量問題
用求順序統計量問題最能說明“分治術” 算法設計思想,所謂順序統計問題是“從有n個元素的序列中選出第k個最小元素”,解此問題最容易想到的辦法是:將這n個元素按從小到大順序排序,然後從排序後的序列中先取第k個元素,即為本問題的解,而排序n個元素最快的排序算法平均需要進行。o(nlogn)次比較,即用排序方法求順序統計量問題的期望時間複雜性為o(nlogn)。通過仔細分析,使用“分而治之”的思想,我們可以找到一個時間耗費為o(n)算法,其算法如下:
Procedure Select(S,K)
Begin
if|S|<50 Then
begin
將S從小到大排序;
Return S 的k 個元素;
end
Eles
begin
把S分為各有5個元素的[|S|/5]個子序列;
如果有剩餘元素,則將剩餘元素作為最後一個子序列;
將每個有5個元素的子序列排序;
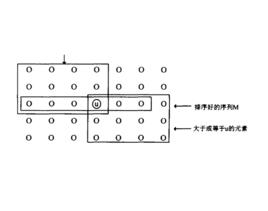
設M是所有5——元素的自序列的中值序列;
U<-Select(M,[M/2]);
設S1、S2、S3是S的分別小於、等於和大於U的元素序列
if|S|>=k Then
Return Select(S1,k)
Eles
if(|S1|+|S2|>=k) Then
Return u
Eles
Return Select(S3,k-|S1|-|S2|)
End