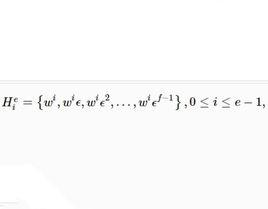基本概念
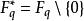 分圓類
分圓類定義1 設q=ef+1為奇素數冪,F為q階有限域,,設w為F的本原元,ε=w 。令
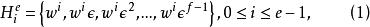 分圓類
分圓類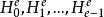 分圓類
分圓類則稱為e次 分圓類(cyclotomic classes)。
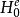 分圓類
分圓類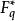 分圓類
分圓類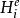 分圓類
分圓類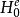 分圓類
分圓類 分圓類
分圓類由定義可知,是的f階乘法子群。而各e次分圓類則是的陪集。以下簡記H =。
定義2 設g=ef+1為奇素數冪,對0≤i,j≤e-1,令
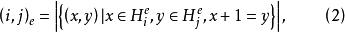 分圓類
分圓類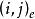 分圓類
分圓類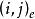 分圓類
分圓類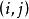 分圓類
分圓類稱為e階分圓數(cyclotomic number),當無需指明e時,也常將簡記為。
分圓類與差集的構作
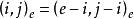 分圓類
分圓類引理1(i);
(ii)
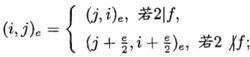 分圓類
分圓類(iii)
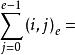 分圓類
分圓類 分圓類
分圓類(iv)
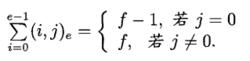 分圓類
分圓類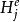 分圓類
分圓類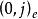 分圓類
分圓類引理2 若且唯若2∈時為奇數。
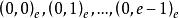 分圓類
分圓類由引理2可知,在這e個分圓數中,恰有1個為奇數,其餘e-1個均為偶數。
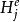 分圓類
分圓類引理3設g∈,則方程
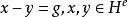 分圓類
分圓類的解的個數恰為(i,0)。
定理1(Lehmer)設q=ef+1為奇素數冪,則分圓類H 為F的加法群中差集的充分必要條件是f為奇數且
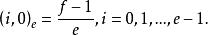 分圓類
分圓類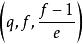 分圓類
分圓類當上述條件滿足時,H 是一個-差集。
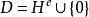 分圓類
分圓類定理2(Lehmer) 設q=ef+1為奇素數冪,則為F的加法群中差集的充分必要條件是f為奇數且
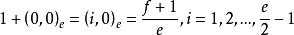 分圓類
分圓類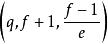 分圓類
分圓類當上述條件滿足時,D是一個-差集。