基本介紹
平面的甚本性質是研究立體幾何的基礎,點、線、面是立體幾何中的最基本的元素,因此共點,共線、共面問題是立體幾何中一類不可忽視的問題。
所謂 共點、共線、共面問題通常指線共點、面共點、點共線、面共線、點共面與線共面問題,證明這類問題常採用共面定理、同一法、向量法等等。
線共點
定義
通過同一點的若干條直線稱為 共點 線,或稱為這些直線共點。
三個平面兩兩相交得到三條交線,這三條交線或交於一點,或相互平行。
證明方法
證明三條或三條以上直線共點的方法有以下幾個(具體例題請參考相應參考資料)。
1.利用特殊點的唯一性
(1)利用已知線段中點,內定比分點,外定比分點的唯一性;
(2)利用已知四邊形對角線交點的唯一性;
(3)利用三角形各心的唯一性。
2.利用三點共線證明三線共點
從一般的意義來說,證明三條直線AB、CD、EF交於一點的問題,可轉化為證明AB和CD的交點P和點F、E三點共線。
3. 利用同一法
要證AB、CD、EF三條直線共點,可設AB與EF交於M,CD與EF交於N,如果證明M和N重合,則AB、CD、EF三線共點。
4. 利用 塞瓦定理 的逆定理
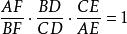 共點
共點△ABC中,D、E、F分別是BC、CA、AB上或延長線上的點,且滿足,則AD、BE、CF交於一點。
5.利用位似圖形
如果能證明兩個圖形是位似圖形,那么對應點的連線共點。
6. 利用笛沙格定理的逆定理
 共點
共點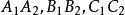 共點
共點△ABC與△ABC在同一平面內,BC與BC的交點為X,CA與CA的交點為Y,AB與AB的交點為Z,且X、Y、Z在一直線上,則三直線交於一點。
7.利用 布列安桑定理
外切於一個非退化的二階曲線的簡單六邊形的三對對頂點的連線交於同一點,這個點稱為布列安桑點 。
例1 設四邊形ABCD的一組對邊BA和CD的延長線交於點E,另一組對邊AD和BC的延長線交於點F,則AC的中點L,BD的中點M及EF的中點N三點共線。
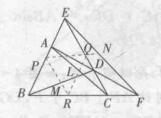 圖1
圖1證明:如圖1所示,設P、Q、R分別為EB、EC、CB的中點,因L、Q、R分別是CA、CE、CB的中點,所以它們在同一直線上,且有
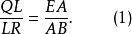 共點
共點同理,M、R、P三點在同一直線上,且
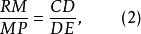 共點
共點N、P、Q三點在同一直線上,且
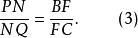 共點
共點(1)×(2)×(3)得
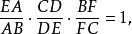 共點
共點所以
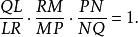 共點
共點因L、M、N三點分別在△PQR三邊或其延長線上,敵由梅涅勞斯定理的逆定理知,L、M、N三點共線。
圓共點
有幾個圓交會於一點時,這些圓叫做 共點的圓。為證若干個圓共點,可先證其中兩圓相交(或相切)於某點,然後再證此點也在其它圓上,這樣,就是把共點圓的問題化為共圓點的問題來研究,現舉例如下:
三點共圓
例2設在△ABC三邊BC、CA、AB所在直線上各任取一點X、Y、Z(如圖2),則三圓AYZ、BZX、CXY共點。
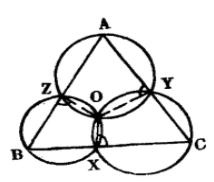 圖2
圖2證明:如圖2所示,⊙BZX與⊙CXY已有一交點X,故當有第二交點O,連OX,OY、OZ,則有∠AYO=∠CXO=∠BZO,因此O點在⊙AYZ上,這就是說,三圓⊙AYZ、⊙BZX、⊙CXY交會於同一點O。
請注意,如果當初X、Y、Z、O各點位置若有更動,不象圖2那樣的話,仍有三圓共點的結論,但證法須作相應的修改,建議讀者自選此種情形,予以試證。此處不再贅述。
四圓共點
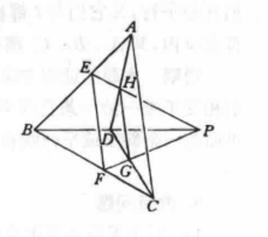
例3 四條直線AE、AF、ED、FB兩兩相交成四個三角形,它們的四個外接圓ABF、BCE,CDF及DAE共點。這點叫做四條直線所構成的完全四邊形的密克點(Miquel)。
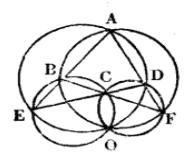 圖3
圖3證明:如圖3,先從△ABF來看,D、E、C是它三邊所在直線上的點,故三圓⊙BCE、⊙CDF、⊙DAE共點(如例2),也就是說,⊙DAE通過⊙BCE與⊙CDF的第二交點O。
再從△DAE來看,B、C、F是它三邊所在直線上的點,所以三圓⊙ABF,⊙BCE、⊙CDF也共點,這就證明了⊙ABF也通過⊙BCE與⊙CDF的交點O。
多個圓共點
介紹一下四條相交直線組成的一個所謂“完全四邊形”,例如AE,AF、BF、DE四條直線(如圖4),它包含三個四邊形:凸的ABCD四邊形,凹的AECF四邊形,折的BEDF四邊形,這樣的四條直線AE、AF、BF、DE組成的圖形就叫做是一個 完全四邊形。其中每個四邊形的對邊都叫做完全四邊形的“對節’’,於是一個完全四邊形共有六雙對節(圖4)。
過完全四邊形每雙對節的中點及它們所在邊的交點作圓,則此六圓共點 。
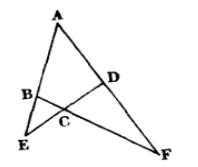 圖4
圖4