簡介
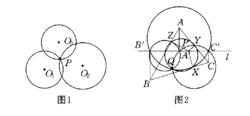共點圓
共點圓 共點圓
共點圓共點圓(concurrent circles)平面幾何術語，指多個圓的一種特殊位置關係.若干圓都通過同一
個點稱為共點圓.如圖1 ,有同一個公共點P，則是共點圓.又如圖2設,分別是△ABC的頂點A,B,C在直線L上的射影，X,Y,Z分別是L上任一點P在BC,CA,AB上的射影，則OXYZ, OXB'C' , OYC'A' , OZA'B‘共點於Q.通過與三角形有關的特定三個垂足點的圓.由一點向三角形每邊所在直線作垂線，通過三垂足的圓稱為該點對於三角形的垂足圓.例如圖2中的OXYZ即點P對於△ABC的垂足圓.
求共點圓
n次操作，每次加入一個以(x,y)為圓心，經過原點的圓，或者詢問一個點是否在所有圓中（包括圓周）。
方法一：
設一個圓的圓心為(a,b)， 一個詢問點為(x,y)，那么(x,y)在圓內或圓周上的條件是：
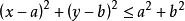共點圓
共點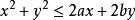圓
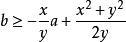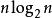共點圓
共點圓也就是說，若一個詢問點在之前的所有圓中，那么對於每個圓心(a,b)都滿足這條式子，而這個式子是一個明顯的半平面形式，即問題變成了，每次加入圓的時候其實是加入一個圓心點，詢問變成是否所有點都在一條直線的上方。我們對操作分治，變成每次把左邊的點加進去，判斷右邊的詢問是否滿足。由於所有詢問都是點在直線上方問題，所以我們可以對點維護下凸包，二分斜率，看看那一個點是否在下面即可。複雜度為O( ) 。
方法二：
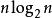共點圓所有的圓都經過同一個點——原點！考慮圓反演，那么我們會得到很多直線，一個點在圓外也就是這個點反演後在直線的上方（這題中圓心都在x軸上方）。這樣問題就變成了是否每個點都被所有半平面包含。這個可以通過求半平面交再三分，二分，或排序之類的得到。複雜度也為O()，但是詢問的主體是不一樣的 。
