八階幻方

美國著名電學家富蘭克林(1706～1790)製作的八階幻方，它有一些獨特的性質： （1）隨意一個2x2的正方形內的數和為130，半行半列數和為130。（幻和為260） （2）3+5+30+28+57+63+40+34=260, 52+45+16+17+54+43+10+23=260. (3)從16到10，加上23到17，和也是260，與“”形平行的數和也為260。角符方向朝左、下、右也是260。

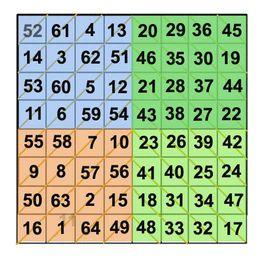
(1)幻方中的64個數字是從1順序增加至64；

(2)每半行、半列上各數和為130(幻和是260)；

(3)幻方角上的四個數與最中心四個數和等於幻和值260；52+45+16+17+54+43+10+23=260；

(4)從16到10，再從23到17所成折線“∧”上八個數字之和也為260；且平行這種折線的諸折線“∧”上的八個數字和也為260。

在丹布朗的小說《失落的秘符》里，哈佛大學符號學家羅伯特·蘭登運用富蘭克林的八階幻方成功破解，原來在金字塔底部的圖案。

八階幻方

八階幻方

按八階幻方把1~64的順序排好變成了因此解開謎題