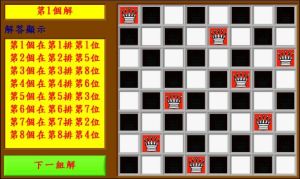
八皇后問題
“八皇后”問題遞歸法求解 (C語言)
/*
八皇后問題是一個古老而著名的問題,是回溯算法的典型例題。該問題是十九世紀著名的數學家高斯1850年提出:在8X8格的西洋棋上擺放八個皇后,使其不能互相攻擊,即任意兩個皇后都不能處於同一行、同一列或同一斜線上,問有多少種擺法。
高斯認為有76種方案。1854年在柏林的象棋雜誌上不同的作者發表了40種不同的解,後來有人用圖論的方法解出92種結果。現代教學中,把八皇后問題當成一個經典遞歸算法例題。
遞歸算法
算法分析:數組a、b、c分別用來標記衝突,a數組代表列衝突,從a~a代表第0列到第7列,如果某列上已經有皇后,則為1,否則為0;
數組b代表主對角線衝突,為b[i-j+7],即從b~b,如果某條主對角線上已經有皇后,則為1,否則為0;
數組c代表從對角線衝突,為c[i+j],即從c~c,如果某條從對角線上已經有皇后,則為1,否則為0;
另最佳化:第一個皇后在1~4格,最後*2,即為總解數
Pascal語言源程式
program queens;
var a:array [1..8] of integer;
b,c,d:array [-7..16] of integer;
t,i,j,k:integer;
procedure print;
begin
t:=t+1;
write(t,': ');
for k:=1 to 8 do write(a[k],' ');
writeln;
end;
procedure try(i:integer);
var j:integer;
begin
if i>8 then print;{完成任務,列印結果}
for j:=1 to 8 do {每個皇后都有8種可能位置}
if (b[j]=0) and (c[i+j]=0) and (d[i-j]=0) then {判斷位置是否衝突}
begin
a[i]:=j; {擺放皇后}
b[j]:=1; {宣布占領第J行}
c[i+j]:=1; {占領兩個對角線}
d[i-j]:=1;
try(i+1); {8個皇后沒有擺完,遞歸擺放下一皇后}
b[j]:=0; {回溯}
c[i+j]:=0;
d[i-j]:=0;
end;
end;
begin
fillchar(a,sizeof(a),0); {初始化數組}
fillchar(b,sizeof(b),0);
fillchar(c,sizeof(c),0);
fillchar(d,sizeof(d),0);
try(1);{從第1個皇后開始放置}
end.
C語言源程式
#include "stdio.h"
static char Queen;
static int a;
static int b;
static int c;
static int iQueenNum=0; //記錄總的棋盤狀態數
void qu(int i); //參數i代表行
int main()
{
int iLine,iColumn;
//棋盤初始化,空格為*,放置皇后的地方為@
for(iLine=0;iLine<8;iLine++)
{
a[iLine]=0; //列標記初始化,表示無列衝突
for(iColumn=0;iColumn<8;iColumn++)
Queen[iLine][iColumn]="*";
}
//主、從對角線標記初始化,表示沒有衝突
for(iLine=0;iLine<15;iLine++)
b[iLine]=c[iLine]=0;
qu(0);
return 0;
}
void qu(int i)
{
int iColumn;
for(iColumn=0;iColumn<8;iColumn++)
{
if(a[iColumn]==0&&b[i-iColumn+7]==0&&c[i+iColumn]==0) //如果無衝突
{
Queen[i][iColumn]="@"; //放皇后
a[iColumn]=1; //標記,下一次該列上不能放皇后
b[i-iColumn+7]=1; //標記,下一次該主對角線上不能放皇后
c[i+iColumn]=1; //標記,下一次該從對角線上不能放皇后
if(i<7) qu(i+1); //如果行還沒有遍歷完,進入下一行
else //否則輸出
{
//輸出棋盤狀態
int iLine,iColumn;
printf("第%d種狀態為:\n",++iQueenNum);
for(iLine=0;iLine<8;iLine++)
{
for(iColumn=0;iColumn<8;iColumn++)
printf("%c ",Queen[iLine][iColumn]);
printf("\n");
}
printf("\n\n");
}
//如果前次的皇后放置導致後面的放置無論如何都不能滿足要求,則回溯,重置
Queen[i][iColumn]="*";
a[iColumn]=0;
b[i-iColumn+7]=0;
c[i+iColumn]=0;
}
}
}
C++語言源程式
#include
#include
#include
int n,k,a,num=0;
int attack(int k){
int flag=0;
int i=1;
while ((ifabs(a[k]-a)!=(k-i))) i++;
if (i==k) flag=1;
return flag;
}
void place(int k)
{
//printf(" %d",k);
int i;
if (k==n+1){
num=num+1;
printf("num=%d:",num);
for (i=1;i
printf(" %d",a);
printf("\n");}
else {
for (i=1;i
a[k]=i;
if (attack(k)==1) place(k+1);
else a[k]=0;
}
}
}
main(){
scanf("%d",&n);
k=1;
place(k);
if (k!=n+1) printf("no solution!\n");
getch();
}
JAVA語言源程式
public class testEghit {
private int[][] a=new int;
private int total=0;
public testEghit() {
init();
}
private void init(){
for(int i=0;i<8;i++){
for(int j=0;j<8;j++){
a[j]=0;
}
}
}
private void suma(){
int sum=0;
for(int i=0;i<8;i++){
for(int j=0;j<8;j++){
sum+=a[j];
}
}
if(sum>7){
total+=1;
System.out.println("sum="+sum);
for(int i=0;i<8;i++){
for(int j=0;j<8;j++){
System.out.print(a[j]+", ");
}
System.out.println("");
}
System.out.println("total="+total);
System.out.println("==============================");
}
// init();
}
private boolean check(int line,int col){
boolean o=false;
for(int i=0;i<8;i++){
if(a[line]==1) return o;
if(a[col]==1) return o;
if((line-i)>-1&&(col-i)>-1){
if(a[line-i][col-i]==1) return o;
}
if((line+i)<8&&(col+i)<8){
if(a[line+i][col+i]==1) return o;
}
if((line-i)>-1&&(col+i)<8){
if(a[line-i][col+i]==1) return o;
}
if((line+i)<8&&(col-i)>-1){
if(a[line+i][col-i]==1) return o;
}
}
return true;
}
private boolean com(int mazz){
boolean o=false;
for(int i=0;i<8;i++){
if(check(8-mazz,i)){
o=true;
a[8-mazz]=1;
if((mazz>1)&&!com(mazz-1)){
o=false;
a[8-mazz]=0;
}
if(mazz==1){
suma();
}
}
a[8-mazz]=0;
}
return o;
}
public static void main(String[] args) {
testEghit t=new testEghit();
t.com(8);
System.out.println("meiy");
}
}
C#語言源程式
[font]using System;
using System.Collections.Generic;
using System.Text;
namespace EightQueen
{
class Program
{
class Eight
{
public int[] result = new int;
public static int amount = 0;
public void PrintResult()
{
Console.Write("Result: ");
foreach (int num in result)
{
Console.Write(num.ToString() + " ");
}
Console.WriteLine("\n");
amount++;
}
}
static void PostQueen(ref Eight eig, int row)
{
if (row > 8 || row < 0)
{
return;
}
// the last pst is at row
// 3 Condition: not same row, not same column, not on the bias line
if (row < 7)
{
for (int i = row + 1; i < 8; i++)
{
int tint = eig.result[row] - eig.result;
if (0 == tint || tint == row - i || tint == i - row )
{
// should not be same column
return;
}
}
}
// if at the last Post
if (0 == row)
{
eig.PrintResult();
return;
}
// iterite to post next
for (int i = 0; i < 8; i++)
{
eig.result[row - 1] = i;
PostQueen(ref eig, row - 1);
}
}
static void Main(string[] args)
{
// Eight queen post on 8*8 grid
Eight eig = new Eight();
PostQueen(ref eig, 8);
Console.WriteLine(string.Format("The total arrange: {0}", Eight.amount));
Console.Read();
}
}
}
C語言實踐編程
#include
#include
int n=8,m0,m1,m2,f; //這裡我先定義是八啦,你們也可以改。
void queen(int k)
{int i;
for(i=1;i<=n;i++)
if(m0[i]!=1&&m1[k+i]!=1&&m2[k-i+n]!=1)
{ m0[i]=1; //設定皇后位置。
m1[k+i]=1;
m2[k-i+n]=1;
if(k
else if(k==n) f++;
m0[i]=0; //清0,重來。
m1[k+i]=0;
m2[k-i+n]=0;
}
}
int main()
{ queen(1);
printf("%d",f);
system("pause");
return 0;
}
說明一下,這只是累加器型的。
[/font]
[font class="Apple-style-span" style="font-style: italic;"]
[/font]
n皇后問題(英文)http://mathworld.wolfram.com/QueensProblem.html
C代碼的另一個例子效率較高
#include "stdio.h"
#include "windows.h"
#define N 8 /* 定義棋盤大小 */
int place(int k); /* 確定某一位置皇后放置與否,放置則返回1,反之返回0 */
void backtrack(int i);/* 主遞歸函式,搜尋解空間中第i層子樹 */
void chessboard(); /* 每找到一個解,列印當前棋盤狀態 */
static int sum, /* 當前已找到解的個數 */
x[N]; /* 記錄皇后的位置,x[i]表示皇后i放在棋盤的第i行的第x[i]列 */
int main(void)
{
backtrack(0);
system("pause");
return 0;
}
int place(int k)
{
/* 測試皇后k在第k行第x[k]列時是否與前面已放置好的皇后相攻擊。 x[j] == */
/* x[k] 時,兩皇后在同一列上;abs(k - j) == abs(x[j] - x[k]) 時,兩皇 */
/* 後在同一斜線上。兩種情況兩皇后都可相互攻擊,故返回0表示不符合條件。*/
for (int j = 0; j < k; j ++)
if (abs(k - j) == abs(x[j] - x[k]) || (x[j] == x[k])) return 0;
return 1;
}
void backtrack(int t)
{
/* t == N 時,算法搜尋至葉結點,得到一個新的N皇后互不攻擊的放置方案 */
if (t == N) chessboard();
else
for (int i = 0; i < N; i ++) {
x
獨立解
在92個解中,很多解在棋盤上有對稱關係,每一個棋子都有8個對稱位置,如果一個解和另外一個解所有的棋子都呈同一種對稱,那么這兩個解之間就是對稱關係。例如右邊兩個解實際上沿著垂直軸翻轉,就是一個,因此不是獨立的。相互間沒有對稱關係的解是獨立解。雖然一個解可以有8個對稱位置,但是有些解經過對稱操作後和沒有操作前是一樣的。
在一個標準的8x8的棋盤中,92個解當中有12個解是獨立的。8x8棋盤的獨立解如圖所示。
如果把棋盤從8X8變成NxN, 八皇后問題就變成了N皇后問題。N從4以上都有解,並分別有相應的獨立解。
下面是皇后的數目於解數目的關係
皇后數: 4 5 6 7 8 9 10 11 12 13 14
獨立解: 1 2 1 6 12 46 92 341 1787 9233 45752
全部解: 2 10 4 40 92 352 724 2680 14200 73712 365596
| 皇后數 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 獨立解 | 1 | 2 | 1 | 6 | 12 | 46 | 92 | 341 | 1787 | 9233 | 45752 |
| 全部解 | 2 | 10 | 4 | 40 | 92 | 352 | 724 | 2680 | 14200 | 73712 | 365596 |
比較特殊的是,皇后6x6棋盤的解比5x5少,其餘解的數目隨著皇后數目增加。但似乎無數學表達式可以描述。
易語言
.版本 2
.支持庫 iext3
.支持庫 iext
.程式集 啟動視窗程式集
.程式集變數 皇后位置數組, 整數型, , "0", 如:皇后位置數組[j]=4,表示第j列,第皇后位置數組[j]行有皇后
.程式集變數 行數組, 整數型, , "0", 行數組[k]=1,表示第k行沒有皇后
.程式集變數 右高左低數組, 整數型, , "0", 右高左低數組[k]=1,表示第k條右高左低的斜線上沒有皇后
.程式集變數 左高右低數組, 整數型, , "0", 左高右低數組[k]=1,表示第k條左高右低的斜線上沒有皇后
.程式集變數 棋盤行列值, 整數型, , , 棋盤規模變數
.子程式 __啟動視窗_創建完畢
' 使用算法:遞歸法
' 問題:N後問題
' 問題描述:
' 西洋棋中皇后可以攻擊所在行,列,斜線上的每一個位置,按照此規則要在一個n*n的棋盤上放n個皇后使每一個皇后都不互相攻擊
' 問題分析:
' (1) 引入1個數組模擬棋盤上皇后的位置
' 皇后位置數組[j]=4,表示第j列,第皇后位置數組[j]行有皇后
' 引入3個工作數組
' 行數組[k]=1,表示第k行沒有皇后
' 右高左低數組[k]=1,表示第k條右高左低的斜線上沒有皇后
' 左高右低數組[k]=1,表示第k條左高右低的斜線上沒有皇后
' 觀察棋盤找到規律
' 同一右高左低的斜線上的方格,它們的行號和列號之和相等;
' 同一左高右低的斜線上的方格,它們的行號和列號只差相等;
' 開始時,所有行和斜線上都沒有皇后,從第一列的第一行配置第一個皇后開始,在第m列的皇后位置數組[m]行放置了一個合理的皇后之後,準備考察第m+1列時,在數組 行數組[],右高左低數組[],左高右低數組[]中為第m列,皇后位置數組[m]的位置設定有皇后標誌
' 如果按此放置位置得不到結果,則把當前列中的有皇后標記改為無皇后標記。
' 依次類推
' 當在棋盤最後一列上也找到合適的位置後得到結果。
' 通過上面規律可以推導出結果。
' 備註:
.子程式 __啟動視窗_尺寸被改變
問題編輯框.寬度 = 高級選擇夾1.寬度 - 16
問題編輯框.高度 = 高級選擇夾1.高度 - 43
分析編輯框.寬度 = 問題編輯框.寬度
分析編輯框.高度 = 問題編輯框.高度
分組框1.寬度 = 高級選擇夾1.寬度 - 18
分組框1.高度 = 高級選擇夾1.高度 - 36
超級列表框1.寬度 = 分組框1.寬度 - 184
超級列表框1.高度 = 分組框1.高度 - 33
.子程式 _計算圖形按鈕_被單擊
.局部變數 局部計次變數, 整數型, , , 在計次循環中記錄循環次數
.局部變數 局部計次變數2, 整數型
.局部變數 返回值, 整數型, , , 返回是否放置所有皇后成功
' 清空列表框
.計次循環首 (超級列表框1.取列數 (), )
超級列表框1.刪除列 (0)
.計次循環尾 ()
.計次循環首 (超級列表框1.取表項數 (), )
超級列表框1.刪除表項 (0)
.計次循環尾 ()
' 獲得輸入棋盤規模數據
棋盤行列值 = 到數值 (輸入編輯框.內容)
.如果真 (棋盤行列值 < 1) ' 棋盤不能為0或負數
輸入編輯框.內容 = “4”
返回 ()
.如果真結束
' 如果輸入的棋盤規模過大提示是否等待
.如果真 (棋盤行列值 > 28)
.如果真 (信息框 (“您輸入的數值過大,處理數據時程式將會有一段時間無回響,是否繼續?”, #是否鈕 + #詢問圖示, “請問:”) ≠ #是鈕)
' 如果不想等待很長時間則返回
返回 ()
.如果真結束
.如果真結束
' 根據的到值定義棋盤行列,定義相關兩斜行的值
重定義數組 (行數組, 假, 棋盤行列值)
重定義數組 (右高左低數組, 假, 2 × 棋盤行列值)
重定義數組 (左高右低數組, 假, 2 × 棋盤行列值)
重定義數組 (皇后位置數組, 假, 棋盤行列值)
' 行數組 =1,表示第1行沒有皇后
.計次循環首 (棋盤行列值, 局部計次變數)
行數組 [局部計次變數] = 1
.計次循環尾 ()
' 右高左低數組=1,表示第1條右高左低的斜線上沒有皇后
' 左高右低數組=1,表示第1條左高右低的斜線上沒有皇后
.計次循環首 (2 × 棋盤行列值, 局部計次變數)
右高左低數組 [局部計次變數] = 1
左高右低數組 [局部計次變數] = 1
.計次循環尾 ()
' 從第一列開始找出合適的放置方法
返回值 = 皇后問題子程式 (1)
.判斷開始 (返回值 = 1)
標籤2.標題 = “找到結果” ' 得到結果顯示在超級列表框中
超級列表框1.插入列 (, “0”, , , , )
超級列表框1.置列寬 (0, 30)
' 畫棋盤列
.計次循環首 (棋盤行列值, 局部計次變數)
超級列表框1.插入列 (, 到文本 (局部計次變數), , , , )
超級列表框1.置列寬 (局部計次變數, 30)
.計次循環尾 ()
' 畫棋盤行
.計次循環首 (棋盤行列值, 局部計次變數)
超級列表框1.插入表項 (, 到文本 (局部計次變數), , , , )
.計次循環尾 ()
' 顯示排列結果
.計次循環首 (棋盤行列值, 局部計次變數)
.計次循環首 (棋盤行列值, 局部計次變數2)
' 如果當前行列坐標上有皇后
.判斷開始 (皇后位置數組 [局部計次變數] = 局部計次變數2)
超級列表框1.置標題 (局部計次變數2 - 1, 局部計次變數, “皇”)
.默認
超級列表框1.置標題 (局部計次變數2 - 1, 局部計次變數, “*”)
.判斷結束
.計次循環尾 ()
.計次循環尾 ()
.默認
標籤2.標題 = “沒有合適結果”
.判斷結束
.子程式 皇后問題子程式, 整數型, , 在n*n棋盤的第k列上找合理的皇后放置位置
.參數 當前判斷列, 整數型, , 當前在試探位置所在的列
.局部變數 局部計次變數, 整數型, , , 試探合理位置時記錄當前的行
.局部變數 結果控制變數, 整數型, , , 找到結果變數為1,沒有結果變數為0
局部計次變數 = 1
結果控制變數 = 0
.判斷循環首 (結果控制變數 = 0 且 局部計次變數 ≤ 棋盤行列值) ' 沒有找到合理的解,並且還有沒試過的行,繼續循環
.如果真 (行數組 [局部計次變數] = 1 且 右高左低數組 [當前判斷列 + 局部計次變數] = 1 且 左高右低數組 [棋盤行列值 + 當前判斷列 - 局部計次變數] = 1) ' 是否在行,列,兩斜線上都沒有放置過皇后
皇后位置數組 [當前判斷列] = 局部計次變數
' 數組值等於 0,表示已經有皇后
行數組 [局部計次變數] = 0
右高左低數組 [當前判斷列 + 局部計次變數] = 0
左高右低數組 [棋盤行列值 + 當前判斷列 - 局部計次變數] = 0
.判斷開始 (當前判斷列 = 棋盤行列值)
返回 (1) ' 如果已經是最後一列,找到解,返回 1
.默認
結果控制變數 = 皇后問題子程式 (當前判斷列 + 1) ' 不是最後列,到下一列去放皇后,返回是否能放置皇后的信息
.判斷結束
行數組 [局部計次變數] = 1
右高左低數組 [當前判斷列 + 局部計次變數] = 1
左高右低數組 [棋盤行列值 + 當前判斷列 - 局部計次變數] = 1
.如果真結束
局部計次變數 = 局部計次變數 + 1
.判斷循環尾 ()
返回 (結果控制變數) ' 返回最終是否有解的信息