基本概念
兩個不重合的平面有一個公共點,叫做這 兩平面相交。
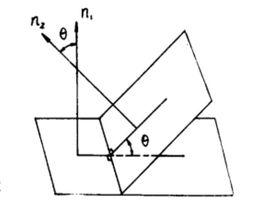
在兩個相交平面的交線上任取一點,經過此點在兩個平面內作交線的垂線,二垂線所夾的銳角成為兩平面的傾角。在兩相交平面之一內作直線與交線成直角,當此直線與另一平面成直角時,則稱兩平面相交成直角 。
兩平面的交角是刻畫相交二平面位置關係的一個數。在空間直角坐標系中,兩平面:
 兩平面相交
兩平面相交 兩平面相交
兩平面相交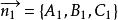 兩平面相交
兩平面相交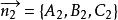 兩平面相交
兩平面相交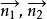 兩平面相交
兩平面相交相交所成二面角用∠(π,π)來表示,兩平面的法向量和的交角設為θ=∠(),則有∠(π,π)=θ或π-θ,故
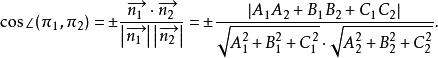 兩平面相交
兩平面相交兩平面相交的分析
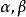 兩平面相交
兩平面相交設兩平面的方程分別為
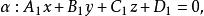 兩平面相交
兩平面相交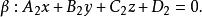 兩平面相交
兩平面相交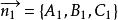 兩平面相交
兩平面相交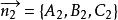 兩平面相交
兩平面相交其法線向量分別為和。
兩平面平行
兩平面平行的充要條件:
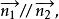 兩平面相交
兩平面相交即
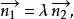 兩平面相交
兩平面相交用分量來表示為:
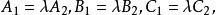 兩平面相交
兩平面相交亦即
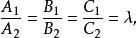 兩平面相交
兩平面相交或
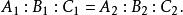 兩平面相交
兩平面相交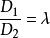 兩平面相交
兩平面相交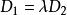 兩平面相交
兩平面相交 兩平面相交
兩平面相交若,即,則平面的方程為:
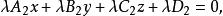 兩平面相交
兩平面相交即:
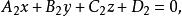 兩平面相交
兩平面相交與平面β的方程一致,所以兩平面重合,由此我們看出:
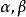 兩平面相交
兩平面相交兩平面平行的充要條件是
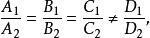 兩平面相交
兩平面相交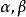 兩平面相交
兩平面相交兩平面重合的充要條件是
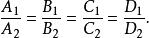 兩平面相交
兩平面相交兩平面相交的充要條件
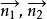 兩平面相交
兩平面相交即不平行,即
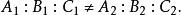 兩平面相交
兩平面相交這時兩平面相交時所得直線的方程可用方程組
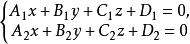 兩平面相交
兩平面相交來表示 。
兩平面的交角
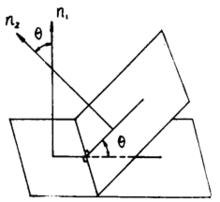 圖1
圖1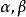 兩平面相交
兩平面相交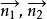 兩平面相交
兩平面相交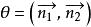 兩平面相交
兩平面相交為了確定起見,規定兩平面組成的二面角中,不大於直角的為兩平面的交角,記作θ,如圖1,所成的夾角θ就是兩法線向量的夾角θ,即(圖1),且
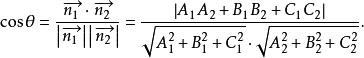 兩平面相交
兩平面相交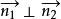 兩平面相交
兩平面相交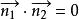 兩平面相交
兩平面相交特別地,當時,, 故又可以得兩平面互相垂直的充要條件為
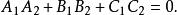 兩平面相交
兩平面相交