概念
全矩陣環(full matrix ring)是一類具體且重要的環。即由矩陣構成的一類有零因子的非交換環。環R上一切n階矩陣的集合{[a]|a∈R}對矩陣的加法和乘法構成的環,稱為R上全矩陣環。也稱它為R上n階矩陣環,記為R或M(R)。全矩陣環的子環稱為矩陣環。域F上全矩陣環F是單環,且是F上矩陣代數,從而也是F上單代數。矩陣環在表示論中有重要意義,F上有限維代數常可用相應的矩陣代數來刻畫。
環
對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
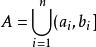 全矩陣環
全矩陣環的全體構成的集類,則F是R上的一個環。環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
環論
一個環是一個集合R,其中有兩個合成運算,叫作加法和乘法,對有序對a,b,a,b∈R,其結果分別用a+b和ab表示,這兩個合成法則滿足:(1)a+b及ab屬於R(閉合);(2)a + b=b + a(交換律);(3) (a+b) + c=a+ (b + c)(結合律);(4)在R中有一個元0叫零元,對R中任意a,適合a + 0 = 0 +a;(5)對R中任意元a,在R中有一個a的負元—a,適合a+ (—a)=0;(6)(ab)c= a(bc);(7)a(b + c)=ab+ac,(b+c)a=ba+ca(分配律),滿足以上條件的代數系即叫環,環論研究的就是具有這些性質的代數系。環論概括了數學各分支中很多基本的特例,如它包括整數環、有理數環、實數環、複數環和各種不同的函式和矩陣環等。環是現代代數中重要概念,其理論和方法在數學許多分支中都有套用。
環論的主要研究內容:①交換環論;②具有鏈條件的環論;③一般環論。1945年雅各布森 (N.Jacobson) 創造了根基理論,建立了一般環構造 的基礎理論。但是到目前為止,質環自身的構造還不夠清楚,甚至有窮環的構造也不清楚,在一般情況 下,理想子環除因子的順序外能否唯一地分解成質理想子環的乘積的問題也沒能徹底解決。近年來,環論的發展很快,大量成果不斷湧現,是目前代數學中最 活躍的分支學科之一。
單環
單環是與群論中單群類相對應的基本環類。一個環(代數)R,若只有平凡理想(即除R和零理想外不含其他理想),則稱R為弱單環或單純環(弱單代數)。弱單環(弱單代數)可分兩類:一類是R≠0,此類環(代數)稱為單環(單代數),它的冪零根為零;另一類是R=0,R稱為零乘環,它的冪零根是R本身.域F上的全矩陣環是單環,也是F上的單代數。F上有限維單代數必含單位元。
表示論
表示論是數學中抽象代數的一支。旨在將代數結構中的元素“表示”成向量空間上的線性變換,藉以研究結構的性質。
略言之,表示論將一代數對象表作較具體的矩陣,並使得原結構中的操作對應到矩陣運算,如矩陣的合成、加法等等。此法可施於群、結合代數及李代數等多種代數結構;其中肇源最早,用途也最廣的是群表示論。設 G 為群,其在域F (常取複數域 F =C)表示是一 F-矢量空間 V 及映至一般線性群之群同態。
假設 V 有限維,則上述同態即是將 G 的元素映成可逆矩陣,並使得群運算對應到矩陣乘法。
表示論的妙用在於能將抽象的代數問題轉為線性代數的操作;若考慮無窮維希爾伯特空間上的表示,並要求一些連續性條件,此時表示論就牽涉到一些泛函分析的課題。
表示論在自然科學中也有套用。對稱性的問題離不開群,而群的研究又有賴於其表示,最明顯的例子便是李群及李代數表示論在量子力學中的關鍵角色。“表示”的概念後來也得到進一步的推廣,例如範疇的表示。
