定義
如果一個矩陣的任何方陣的行列式等於1,-1或0,則稱該矩陣為全單位模矩陣(total unimodular matrix)。
不難知道,全單位模矩陣的一個明顯的必要條件是它的元素為1,-1或0,下面的定理給出了全單位模矩陣的一個充分條件。
 全單位模矩陣
全單位模矩陣 全單位模矩陣
全單位模矩陣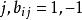 全單位模矩陣
全單位模矩陣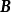 全單位模矩陣
全單位模矩陣定理1 設 ,且對一切 和 或0,如果下面兩個條件都滿足,則 是全單位模矩陣。
(1) B的每一列最多有兩個非零元素;
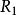 全單位模矩陣
全單位模矩陣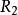 全單位模矩陣
全單位模矩陣(2) B的行可分劃成兩個子集 和 ,使得對於同一列中兩個非零元素,當這兩個非零元素符號相同時,對應的兩行在不同的行子集中;當符號不同時,對應的兩行在同一行子集中。
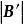 全單位模矩陣
全單位模矩陣證明: 用歸納法證明。只需證明 B的任何一個子方陣 B'的行列式=1,-1或0,設 B'是n階方陣,對n進行歸納.若n=1時,則顯然成立。
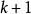 全單位模矩陣
全單位模矩陣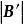 全單位模矩陣
全單位模矩陣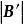 全單位模矩陣
全單位模矩陣 全單位模矩陣
全單位模矩陣由於 B滿足(1)和(2),因此 B的任何子矩陣也滿足這兩個條件,假設 B的任何k階子方陣的行列式等於1,-1或0,任取 B的階子方陣 B',它也滿足條件(1)和(2),如果 B'的某一列恰有一個非0元素,記該元素在 B'中的餘子式為b,則=±b,由歸納假設,b=1,-1或0,從而=1,-1或0;如果 B'的每一列恰有兩個非零元素,則對 B'中任何列,有
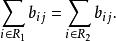 全單位模矩陣
全單位模矩陣 全單位模矩陣
全單位模矩陣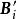 全單位模矩陣
全單位模矩陣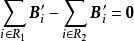 全單位模矩陣
全單位模矩陣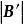 全單位模矩陣
全單位模矩陣把 B'的第行記為,則,即 B'的所有行向量是線性相關的,故=0 。
相關性質
定理2非空無環有向圖的關聯矩陣是全單位模的。
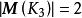 全單位模矩陣
全單位模矩陣順便指出:圖的關聯矩陣不一定是全單位模矩陣,例如。
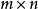 全單位模矩陣
全單位模矩陣定理3 全單位模矩陣 A有下列性質:
 全單位模矩陣
全單位模矩陣(1) 的任何子矩陣是全單位模矩陣。
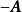 全單位模矩陣
全單位模矩陣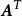 全單位模矩陣
全單位模矩陣(2) 和 是全單位模矩陣。
(3) 把 A的兩行互換得到的矩陣是全單位模矩陣。
(4) 把 A的兩列互換得到的矩陣是全單位模矩陣。
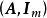 全單位模矩陣
全單位模矩陣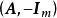 全單位模矩陣
全單位模矩陣(5) 和 是全單位模矩陣。
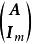 全單位模矩陣
全單位模矩陣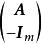 全單位模矩陣
全單位模矩陣(6) 和 是全單位模矩陣。
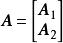 全單位模矩陣
全單位模矩陣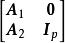 全單位模矩陣
全單位模矩陣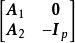 全單位模矩陣
全單位模矩陣(7) 設 ,則 和 是全單位模矩陣。
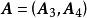 全單位模矩陣
全單位模矩陣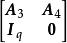 全單位模矩陣
全單位模矩陣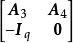 全單位模矩陣
全單位模矩陣(8) 設 ,則 和 是全單位模矩陣。
證明:性質(1)、(2)、(3)、(4) 是顯然的。
下證(5)。
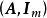 全單位模矩陣
全單位模矩陣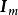 全單位模矩陣
全單位模矩陣設 B是 的任一非奇異子矩陣,若 B是 A或 的子矩陣,則 B的行列式的絕對值|det B|=1;否則,設
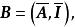 全單位模矩陣
全單位模矩陣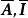 全單位模矩陣
全單位模矩陣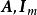 全單位模矩陣
全單位模矩陣這裡 分別是 的子矩陣。互換 B的某些行可得
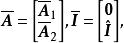 全單位模矩陣
全單位模矩陣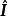 全單位模矩陣
全單位模矩陣其中 為單位矩陣。記
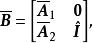 全單位模矩陣
全單位模矩陣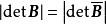 全單位模矩陣
全單位模矩陣注意到 ,並且
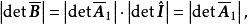 全單位模矩陣
全單位模矩陣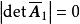 全單位模矩陣
全單位模矩陣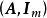 全單位模矩陣
全單位模矩陣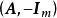 全單位模矩陣
全單位模矩陣由於 A是全單位模矩陣,故 或1,又因 B是非奇異矩陣,所以|det B|=1,這就證明了 是全單位模矩陣。同理可證: 也是全單位模矩陣。
由(2)和(5)知,(6)成立。
根據證明(5)的類似推理,不難證明(7)。
(8)可以由(2)和(7)得到。
關於整數線性規劃問題
網路最最佳化的許多問題常常可以用一個整數線性規劃模型來描述。整數線性規劃是指要求變數取整數值的線性規劃 。
考慮整數線性規劃問題
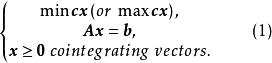 全單位模矩陣
全單位模矩陣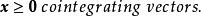 全單位模矩陣
全單位模矩陣 全單位模矩陣
全單位模矩陣這裡,“ ”是指 的每個分量都是非負整數。所有元素均是整數的矩陣稱為整數矩陣。所有分量都是整數的向量稱為整向量。我們假定(1)式中的 A是整數矩陣, b是整向量。
在整數線性規劃問題(1)式中去掉整數約束就得到線性規劃問題
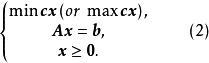 全單位模矩陣
全單位模矩陣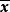 全單位模矩陣
全單位模矩陣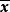 全單位模矩陣
全單位模矩陣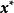 全單位模矩陣
全單位模矩陣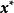 全單位模矩陣
全單位模矩陣如果(2)式的可行解 是整向量,則稱 為(2)式的整數解。如果(2)式的最優解 是整數解。則稱 是(2)式的最優整數解。因此,整數線性規劃問題(1)式的求解可以化為求線性規劃問題(2)式的最優整數解。
定理4 設 A為行滿秩整數矩陣,則下面三個條件等價:
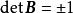 全單位模矩陣
全單位模矩陣(i) A的任意基矩陣 B的行列式 ;
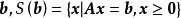 全單位模矩陣
全單位模矩陣(ii) 對於任意整向量 的極點的每個分量都是整數。
(iii) A的任何基矩陣 B的逆矩陣 B 都是整數矩陣。
定理5 設 A是全單位模矩陣,如果線性規劃問題(2)式有最優解,則(2)式必有最優整數解 。
由定理5知,若 A是全單位模矩陣,則整數線性規劃問題(1)式中的整數約束可以去掉而化為線性規劃問題(2)式來求解。
考慮整數線性規劃問題問題
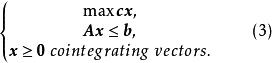 全單位模矩陣
全單位模矩陣這裡 A是整數矩陣, b是整向量。它對應的線性規劃問題為
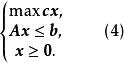 全單位模矩陣
全單位模矩陣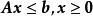 全單位模矩陣
全單位模矩陣因為等價於
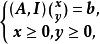 全單位模矩陣
全單位模矩陣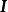 全單位模矩陣
全單位模矩陣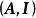 全單位模矩陣
全單位模矩陣其中是單位矩陣。並且由定理3中的(5)和(1)知: A為全單位模矩陣若且唯若為全單位模矩陣。
定理6 設 A是全單位模矩陣,則整數線性規劃問題(3)式中的整數約束可以去掉而化為線性規劃問題(4)式。
定理5和定理6是整數線性規劃中兩個重要的結論,它們表明:在一定條件下,整數線性規劃可以化為線性規劃來解。這就大大簡化了整數線性規劃的求解 。

