簡介
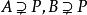 素環
素環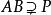 素環
素環設 R 為環,P 為 R 的理想。若對於 R 的任意理想 都有 ,則稱 P 為 R 的一個素理想(prime ideal)。若零理想是環 R 的素理想,則稱 R 為一個素環。例:非交換整環、單環、(左或右)本原環為素環。
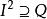 素環
素環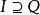 素環
素環若環 R 的理想 Q 滿足:對於使得 的任意理想 I 都有 ,則稱 Q 是 R 的半素理想。若 R 的零理想是半素理想,則稱 R 為半素環(semiprime ring)。環 R 為半素環若且唯若 R 為素環當次直積,若且唯若 R 中所有素理想的交為零。
準素環
定義
若局部環R的雅各布森根是冪零的,則稱R為完全準素環(completely primary ring)。
完全準素環R上的全矩陣環稱為準素環。
若半局部環R的雅各布森根是冪零的,則稱R為半準素環(semiprimary ring)。
麼環R為左阿廷環若且唯若它既是左諾特又是半準素環。
性質
準素環是接近素環的特殊環類。一個有單位元的交換環R,若它最多含一個素理想P,則稱R為準素環。
例如,域是準素環。
若交換環R的準素理想Q有極大理想M作為其相伴素理想,則R/Q也是準素環。
任意滿足降鏈條件的有1交換環R,可惟一分解為諾特準素環的直和。

