總體介紹
全局漸近穩定性是一類全相空間均為吸引區域的漸近穩定性。考慮微分方程組
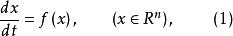 全局漸近穩定性
全局漸近穩定性 全局漸近穩定性
全局漸近穩定性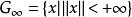 全局漸近穩定性
全局漸近穩定性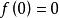 全局漸近穩定性
全局漸近穩定性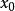 全局漸近穩定性
全局漸近穩定性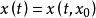 全局漸近穩定性
全局漸近穩定性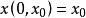 全局漸近穩定性
全局漸近穩定性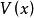 全局漸近穩定性
全局漸近穩定性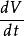 全局漸近穩定性
全局漸近穩定性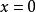 全局漸近穩定性
全局漸近穩定性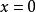 全局漸近穩定性
全局漸近穩定性其中 在域 上定義且連續並滿足局部李普希茨條件,同時設 ,因此,對任何初始值 ,存在(1)的惟一的解 滿足 。由李亞普諾夫第二方法知道,如果存在一個定正函式 ,它關於(1)的導數 是定負的,那么,方程(1)的奇點 是漸近穩定的,方程組(1)的奇點 的吸引區域(或稱漸近穩定性區域)是所有具有性質
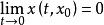 全局漸近穩定性
全局漸近穩定性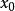 全局漸近穩定性
全局漸近穩定性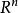 全局漸近穩定性
全局漸近穩定性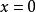 全局漸近穩定性
全局漸近穩定性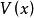 全局漸近穩定性
全局漸近穩定性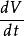 全局漸近穩定性
全局漸近穩定性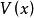 全局漸近穩定性
全局漸近穩定性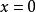 全局漸近穩定性
全局漸近穩定性的點 的集合。如果吸引區域是整個相空間 ,則 被稱為 全局漸近穩定的,這時下面的結論成立:如果存在定正函式 ,它關於(1)的導數 是定負的,並且 是徑向無界的,則奇點 是全局漸近穩定的,李亞普諾夫(А.М.Ляпунов,)原來只考慮原點附近即局部的穩定性,克拉索夫斯基(Н.Н.Красовский)將其推廣為全相空間,即全局的穩定性 。
相關概念及定理
平衡狀態
考慮如下非線性動態系統(可以是控制量保持不變的被控對象,也可以是包括被控對象和控制器在內的閉環系統)的狀態方程
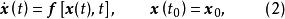 全局漸近穩定性
全局漸近穩定性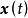 全局漸近穩定性
全局漸近穩定性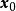 全局漸近穩定性
全局漸近穩定性 全局漸近穩定性
全局漸近穩定性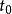 全局漸近穩定性
全局漸近穩定性式中, 為n維狀態向量; 為初始狀態; 為連續時間變數; 為初始時刻 。
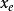 全局漸近穩定性
全局漸近穩定性如果狀態空間存在某一狀態 滿足
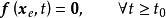 全局漸近穩定性
全局漸近穩定性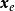 全局漸近穩定性
全局漸近穩定性則稱 是系統的一個 平衡狀態,也稱 平衡點。也就是說,只要無外力作用於系統,存平衡點處系統狀態的變化速度為0,系統將永遠保持在這個平衡狀態上。
穩定性
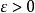 全局漸近穩定性
全局漸近穩定性 全局漸近穩定性
全局漸近穩定性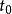 全局漸近穩定性
全局漸近穩定性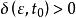 全局漸近穩定性
全局漸近穩定性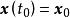 全局漸近穩定性
全局漸近穩定性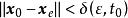 全局漸近穩定性
全局漸近穩定性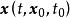 全局漸近穩定性
全局漸近穩定性如果對於任意給定實數 ,存在一個與 和 有關的實數 ,只要初始狀態 滿足 ,系統狀態方程式(2)的解 滿足
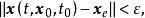 全局漸近穩定性
全局漸近穩定性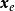 全局漸近穩定性
全局漸近穩定性那么,稱系統的平衡點 是Lyapunov意義下穩定的。
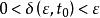 全局漸近穩定性
全局漸近穩定性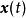 全局漸近穩定性
全局漸近穩定性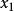 全局漸近穩定性
全局漸近穩定性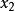 全局漸近穩定性
全局漸近穩定性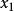 全局漸近穩定性
全局漸近穩定性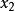 全局漸近穩定性
全局漸近穩定性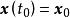 全局漸近穩定性
全局漸近穩定性注釋: 定義中實數 通常有 ,定義的直觀含義是,在系統受到較小的初始擾動後。系統運動的軌線不會偏離平衡點很遠。在二維情況下,設, 的分量分別是 和 ,那么在 和 組成的二維狀態空間平面中.狀態方程式(2)的解就是起點為 的一條連續的運動軌跡。定義所指的Lyapunov意義下穩定的含義如圖1(a)所示。
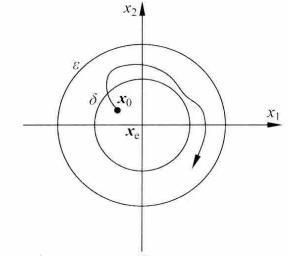 圖1(a) 穩定
圖1(a) 穩定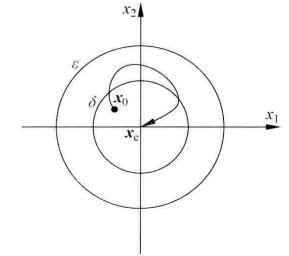 圖1(b)漸近穩定
圖1(b)漸近穩定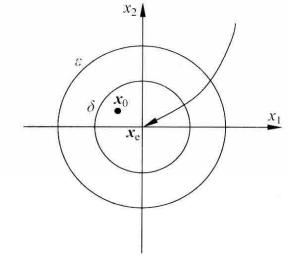 圖1(c) 全局漸近穩定
圖1(c) 全局漸近穩定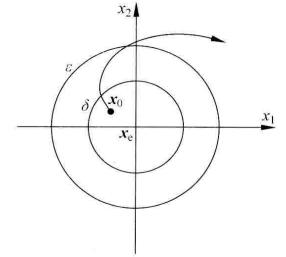 圖1(d)不 穩定
圖1(d)不 穩定另外,凡是不滿足穩定性定義的系統是不穩定系統,其直觀意義如圖1(d)所示。
漸近穩定性
連續時變非線性系統的狀態空間模型的一般形式為
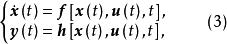 全局漸近穩定性
全局漸近穩定性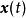 全局漸近穩定性
全局漸近穩定性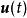 全局漸近穩定性
全局漸近穩定性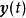 全局漸近穩定性
全局漸近穩定性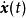 全局漸近穩定性
全局漸近穩定性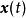 全局漸近穩定性
全局漸近穩定性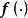 全局漸近穩定性
全局漸近穩定性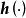 全局漸近穩定性
全局漸近穩定性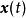 全局漸近穩定性
全局漸近穩定性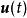 全局漸近穩定性
全局漸近穩定性式中, 為n維狀態變數, 和 分別為系統的輸入和輸出向量;t為連續時間變數; 為 對時間t的一階導數; 和 分別為關於 和 的有界、連續可微的非線性向量函式;n為系統的階次。
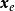 全局漸近穩定性
全局漸近穩定性如果式(3)所示動態系統的一個平衡狀態 滿足
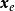 全局漸近穩定性
全局漸近穩定性(1) 是Lyapunov意義下穩定的;
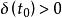 全局漸近穩定性
全局漸近穩定性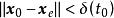 全局漸近穩定性
全局漸近穩定性(2) 存在一個實數 ,使得只要初始狀態滿足 ,就有
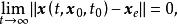 全局漸近穩定性
全局漸近穩定性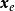 全局漸近穩定性
全局漸近穩定性則稱 是 漸近穩定的。
注釋: 定義的含義是一切由平衡點的,個小的鄰域m發的運動軌線,最終都將收斂到平衡點處,如圖1(b)所示。
全局漸近穩定性的意義
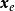 全局漸近穩定性
全局漸近穩定性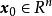 全局漸近穩定性
全局漸近穩定性如果式(3)所示動態系統的一個平衡狀態 對所有 有
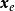 全局漸近穩定性
全局漸近穩定性① 是穩定的;
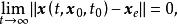 全局漸近穩定性
全局漸近穩定性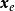 全局漸近穩定性
全局漸近穩定性② 則稱 是全局漸近穩定的。
注釋: 定義的直觀解義如圖1(c)所示。對於線性系統而言,一個線性系統如果是漸近穩定的,則必然是全局漸近穩定的。
上述各種穩定性定義之間的包含關係如圖2所示 。
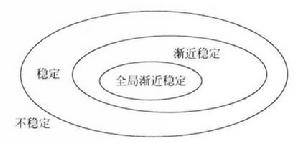 圖2 各種穩定性定義之間的關係
圖2 各種穩定性定義之間的關係