簡介
在同圓內,四邊形的四個頂點均在同一個圓上的四邊形叫做圓內接四邊形,擁有很多有用的性質。
性質定理
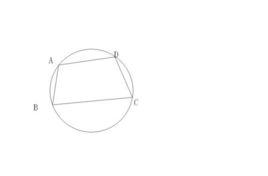
以圓內接四邊形ABCD為例,圓心為O,延長AB至E,AC、BD交於P,則:
▶圓內接四邊形的對角互補:∠BAD+∠DCB=180°,∠ABC+∠ADC=180°
▶圓內接四邊形的任意一個外角等於它的內對角:∠CBE=∠ADC
▶圓心角的度數等於所對弧的圓周角的度數的兩倍:∠AOB=2∠ACB=2∠ADB
▶同弧所對的圓周角相等:∠ABD=∠ACD
▶圓內接四邊形對應三角形相似:△ABP∽△DCP(三個內角對應相等 )
▶相交弦定理:AP×CP=BP×DP
▶托勒密定理:AB×CD+AD×CB=AC×BD
判定定理編輯
1、如果一個四邊形的對角互補,那么這個四邊形內接於一個圓;
2、如果一個四邊形的外角等於它的內對角,那么這個四邊形內接於一個圓;
3、如果一個四邊形的四個頂點與某定點等距離,那么這個四邊形內接於以該點為圓心的一個圓;
4、若有兩個同底的三角形,另一頂點都在底的同旁,且頂角相等,那么這兩個三角形有公共的外接圓;
5、如果一個四邊形的張角相等,那么這個四邊形內接於一個圓;
面積計算編輯
S圓內接四邊形=√[﹙p-a﹚﹙p-b﹚﹙p-c﹚﹙p-d﹚],[p=1/2﹙a+b+c+d﹚],此公式叫婆羅摩笈多公式。
熟悉海倫公式的可以看出,這和海倫公式三角形面積S=√[p ﹙p-a﹚﹙p-b﹚﹙p-c﹚] (p=1/2﹙a+b+c﹚)具有驚人的相似,其實海倫公式就是婆羅摩笈多公式d=0的特殊形式。
相關例題編輯
例題1
在圓內接四邊形ABCD中,AB=3,AD=5,BD=7,∠BDC=45°,則BC的長為?
答案
使用餘弦定理:BD2=AB2+AD2-2AB×AD×cosA,解得∠A=120°,
因為:圓內接四邊形對角互補,
所以:∠C=60°,
使用正弦定理: BC÷sin∠BDC=BD÷sin∠C,
即BC÷[(√2)÷2]=7÷[(√3)/2]
所以:BC=(7√6)/3[2]
例題2:
在梯形ABCD中,AB//DC,AB>CD,K、M分別在AD、BC上,∠DAM=∠CBK,
求證:∠DMA=∠CKB(第二屆袓沖之杯國中數學競賽考題)
答案
證明:聯結KM與BC延長線上一點E。
因為:∠DAM=∠CBK
所以:AKMB四點共圓
因為:AB//DC
所以:∠DKM=∠MBA =∠DCE
所以:∠AKB=∠AMB,∠DKM=∠MBA
所以:CDKM四點共圓
所以:∠DKC=∠CMD
所以:∠CKB=∠DMA