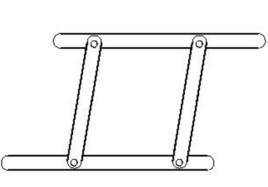
基本概念
如果四邊形的四條邊的邊長一定，其四個內角不固定，這樣的四邊形就叫做鉸鏈四邊形，鉸鏈四邊形的任三邊長度之和大於第四邊，鉸鏈四邊形還有一個重要的性質：在四邊長度給定的一切四邊形中，內接於圓的四邊形具有最大的面積。
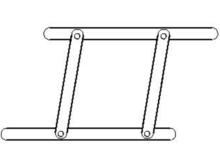圖1相關定理
我們知道，一個三角形在三邊長度給定的條件下，這個三角形的形狀及它的面積就被惟一地確定下來，但對四邊形來講，情況就大不相同了，當四邊長度給定時，可以做出各種各樣形狀的四邊形。譬如，我們取長度分別為a、b、c、d的四根小木條，並用鉸鏈聯成一個活動的四邊形(圖2)，活動這個四邊形的頂角。便可得到各種形狀的四邊形，這些四邊形具有不同的面積。那么在這些四邊形中，怎么樣的四邊形具有最大的面積?
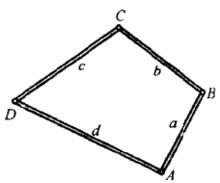圖2下面的定理回答了這個問題（關於定理的證明請參考相應書籍 ）。
定理1 在四邊長度給定的一切四邊形中，內接於圓的四邊形具有最大的面積。
細心的讀者可能會提出這樣的問題：難道在邊長給定的條件下，適當調整夾角一定能使四邊形內接於圓嗎?
引理 在保持四邊形各邊長度的條件下，適當調整它的頂角，一定能夠使它內接於圓 。
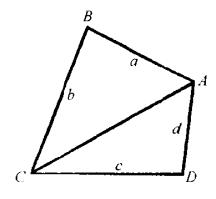圖3鉸鏈四邊形的面積
當四邊長度給定時，四邊形面積的最大值
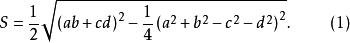鉸鏈四邊形這也就是四邊給定且又內接於圓的一般四邊形的面積公式 。
設a+b+c+d=2p，公式(1)能改寫成更對稱更完整且便於記憶的形式
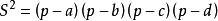鉸鏈四邊形或
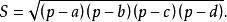鉸鏈四邊形這個關於a、b、c、d具有對稱形式的公式還告訴我們:面枳的最大值與給定邊的次序無關，僅由給定的邊長a、b、c、d惟一確定。
假如四辺形ABCD的邊長中有一邊的長度逐漸縮短而最後趨於零，譬如DA=d=0，此吋，四邊形退化為三角形，任何三角形都內接於圓，故得三角形面積
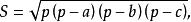鉸鏈四邊形
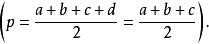鉸鏈四邊形這就是著名的 海倫公式。因此，上述公式是海倫公式的推廣。
公式(1)：
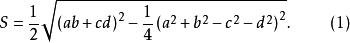鉸鏈四邊形是我國南宋數學家秦九韶在他所著《數書九章》中的三斜求積(已知三邊求三角形的面積)公
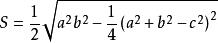鉸鏈四邊形的推廣 。
