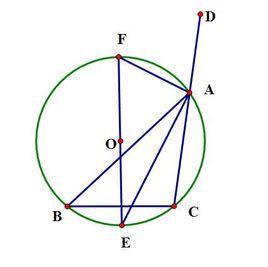
定義
三頂點都在一個圓周上的三角形,叫做這個圓周的 內接三角形,而這個圓周叫做該三角形的 外 接圓。任何一個三角形都有且僅有一個外接圓,外接圓的中心是三角形三邊 中垂線的交點;如果三角形是銳角三角形時,那么外接圓的中心在三角形的內部,如果是鈍角三角形時,那么外接圓的中心則在三角形的外部,在直角三角形時,外接圓的中心則是斜邊的中點。
三角形外接圓的半徑計算公式為:
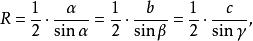 內接三角形
內接三角形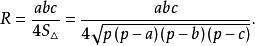 內接三角形
內接三角形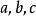 內接三角形
內接三角形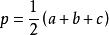 內接三角形
內接三角形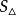 內接三角形
內接三角形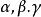 內接三角形
內接三角形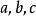 內接三角形
內接三角形其中 是三角形的邊; 是半周長, 是三角形的面積; 分別是三角形的邊 所對的內角。
外切三角形:三邊都與一個圓相切的三角形叫做這個圓的外切三角形,而這個圓叫做該三角形的 內切圓。在任何一個三角形里,都能作且只能作一個內切圓,內切圓的中心O是三角形的 內角平分線的交點。三角形內切圓的半徑計算公式為:
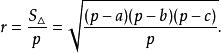 內接三角形
內接三角形相關證明題舉例
1.如圖,已知在△ABC中,AD和BD分別平分∠BAC和∠ABC,延長AD交△ABC外接圓於E,連結BE,求證:BE=DE。
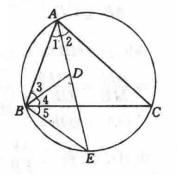 圖1
圖1證明: 如圖,
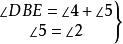 內接三角形
內接三角形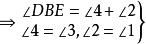 內接三角形
內接三角形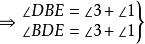 內接三角形
內接三角形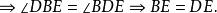 內接三角形
內接三角形說明: 三角形內角平分線的交點是三角形的 內心,所以本題可敘述為如下命題:“ 三角形一個角所對外接圓圓弧的中點到另外兩個角的頂點的距 離。等於它到這個三角形的內心的距離.”
2.如圖,已知圓O是△ABC的外接圓,AD⊥BC於D,AE平分∠BAC,交圓O於E,求證:AE平分∠OAD。
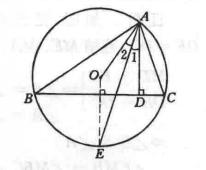 圖2
圖2證明: 如圖,連結OE。
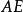 內接三角形
內接三角形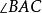 內接三角形
內接三角形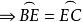 內接三角形
內接三角形平分
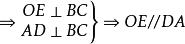 內接三角形
內接三角形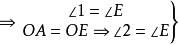 內接三角形
內接三角形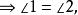 內接三角形
內接三角形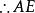 內接三角形
內接三角形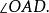 內接三角形
內接三角形平分
說明: 圖中從頂點A引出的三條線段AO、AE、AD分別經過△ABC的 外心、 內心、 垂心,所以本題給出了聯繫三角形外心、內心、垂心的一個幾何性質。
3.如圖,已知H、O分別是△ABC的垂心和外心,OL⊥BC於L,求證:AH=2OL。
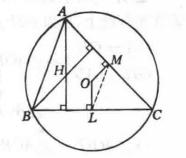 圖3
圖3證明: 如圖,作OM⊥AC於M,則M是AC的中點,連結ML。
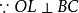 內接三角形
內接三角形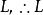 內接三角形
內接三角形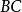 內接三角形
內接三角形於 是 的中點,
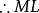 內接三角形
內接三角形是△ABC的一條中位線,
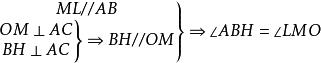 內接三角形
內接三角形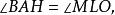 內接三角形
內接三角形同理,
 內接三角形
內接三角形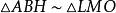 內接三角形
內接三角形 內接三角形
內接三角形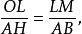 內接三角形
內接三角形 內接三角形
內接三角形又 LM是△ABC的中位線,
 內接三角形
內接三角形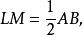 內接三角形
內接三角形 內接三角形
內接三角形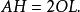 內接三角形
內接三角形說明: (1)構造兩個三角形相似,利用相似比來證等比式是本題證明的思路。
(2)本題可敘述為關於三角形垂心和外心的一個命題:“ 三角形垂心到 一個角的頂點的距離等於外心到這個角對邊距離的兩倍”。
相關定理
①三角形的外接圓有關定理:三角形各邊垂直平分線的交點,是外心。外心到三角形各頂點的距離相等。外心到三角形各邊的垂線平分各邊。
② 三角形的內切圓有關定理:三角形各內角平分線的交點,是內心。內心到三角形各邊的距離相等。三角形任一頂點到內切圓的兩切線長相等。三角形頂點到內切圓的切線長,是這點到圓心的距離與它圓外部分的比例中項。