元素法

元素法也叫微元法，是分析、解決物理問題中的常用方法，也是從部分到整體的思維方法。用該方法可以使一些複雜的物理過程用我們熟悉的物理規律迅速地加以解決，使所求的問題簡單化。在使用元素法處理問題時，需將其分解為眾多微小的“元過程”，而且每個“元過程”所遵循的規律是相同的，這樣，我們只需分析這些“元過程”，然後再將“元過程”進行必要的數學方法或物理思想處理，進而使問題求解。使用此方法會加強我們對已知規律的再思考，從而引起鞏固知識、加深認識和提高能力的作用。

基本信息

• 中文名：元素法
• 英文名：atomistic approac

• 別名：微元法
• 作用：分析與解決物理問題中的常用方法

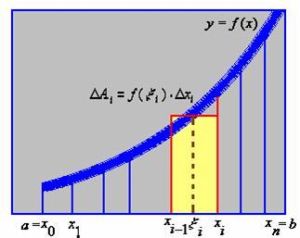
微元法

微元法是指在處理問題時，從對事物的極小部分(微元)分析入手，達到解決事物整體目的的方法。它在解決物理學問題時很常用，思想就是“化整為零”，先分析“微元”，再通過“微元”分析整體。

引言

這是一種深刻的思維方法，是先分割逼近，找到規律，再累計求和，達到了解整體。是對某事件做整體的觀察後，取出該事件的某一微小單元進行分析，通過對元素的細節的物理分析和描述，最終解決整體的方法。例如，分析勻速圓周運動的向心加速度，根據加速度的定義，對圓周運動的速度變化進行元素分析，可以推導出向心加速度的表達式。

引入介紹

元素法

在高中物理中，由於數學學習上的局限，對於高等數學中可以使用積分來進行計算的一些問題，在高中很難加以解決。例如對於求變力所做的功或者對於物體做曲線運動時某恆力所做的功的計算；又如求做曲線運動的某質點運動的路程，這些問題對於中學生來講，成為一大難題。但是如果套用積分的思想，化整為零，化曲為直，採用“元素法”，可以很好的解決這類問題。“元素法”通俗地說就是把研究對象分為無限多個無限小的部分，取出有代表性的極小的一部分進行分析處理，再從局部到全體綜合起來加以考慮的科學思維方法，在這個方法裡充分的體現了積分的思想。高中物理中的瞬時速度、瞬時加速度、感應電動勢等等，都是用這種方法定義的。

取元原則

選取元素時所遵從的基本原則是由於所取的“元素”最終必須參加疊加演算，所以，對“元素”及相應的量的最基本要求是：應該具備“可加性”特徵；為了保證所取的“元素”在疊加域內能夠較為方便地獲得“不遺漏”、“不重複”的完整疊加，在選取“元素”時，就應該注意：按照關於量的某種“序”來選取相應的“元素”；疊加演算實際上是一種的複雜的“加權疊加”。對於一般的“權函式”來說，這種疊加演算（實際上就是要求定積分）極為複雜，但如果“權函式”具備了“平權性”特徵（在定義域內的值處處相等）就會蛻化為極為簡單的形式。

換元技巧

就“元素法”的套用技巧而言，最為關鍵的是要掌握好換“元”的技巧。因為通常的解題中所直接選取的“元素”並不一定能使“權函式”滿足“平權”的條件，這將會給接下來的疊加演算帶來困難，所以，必須運用換“元”的技巧來改變“權函式”，使之具備“平權性”特徵以遵從取元的“平權性原則”。

最常見的換“元”技巧有如下幾種：

（1）“時間元”與“空間元”間的相互代換（表現時、空關係的運動問題中最為常見）；

（2）“體元”、“面元”與“線元”間的相互代換（實質上是降“維”）；

（3）“線元”與“角元”間的相互代換（“元”的表現形式的轉換）；

（4）“孤立元”與“組合元”間的相互代換（充分利用“對稱”特徵）。