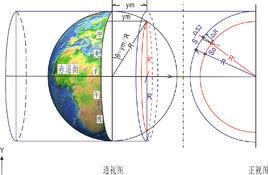
長度投影變形成因分析
橢球面是一個不可展平的凸起的曲面,將這個曲面上的元素(距離、方向、角度、圖形)歸算到平面上,必然同曲面上的對應元素(距離、方向、角度、圖形)產生差異,這一差異稱之為投影變形。
長度投影變形 ,主要有兩項構成,一項為 高程歸化改正,一項為 高斯投影變形。將地面觀測值先歸算到參考橢球面(或大地水準面)上,在變換過程中長度發生的變形,叫做高程歸化改正。然後再從參考捕球面歸化到高斯平面上,在變換過程中長度發生的變形,叫做高斯投影變形。控制長度投影變形就是控制高程歸化改正和高斯投影變形的綜合變形影響。
從設計平面(如1:2000地形圖)上坐標反算距離(高斯平面長度)歸化到參考橢球面(高斯投影變形Δ S),再將參考橢球面上的長度歸化到地面實際長度(高程歸化變形Δ S)。
高程歸化改正產生的變形
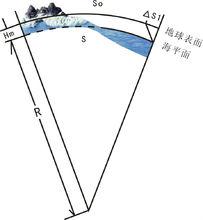 允差分析法
允差分析法測量是在地球表面進行,計算要歸算到海平面上,距離必然發生變化,這就是高程投影變形△ S。海平面上距離 S永遠小於地球表面距離 S,測量區域所在地球表面高程越高,產生的變形也越大。
Δ S=- S× H÷R
高斯-克呂格投影產生的變形
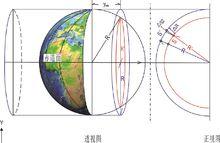 允差分析法
允差分析法圖2.3藍色外圓為橫軸圓筒的紙面,紅色內圓為 ym(距中央子午線緯度方向的距離)處為地球平行中央子午線橫切面,光線垂直紙面射向圓柱中軸(絕非地球球心)。
Δ S= S×0.5×( y÷R)²
對以上兩式求和即為長度投影綜合變形,將距離由較高的高程面歸算至較低的橢球面時,長度總是減小的,公式表明,將橢球面上的距離投影至高斯平面時,長度總是增加的。
允差分析法
基本構思
考慮到勘測、設計人員和施工人員不同的技術特點,在完成道路選線可行性研究報告後,根據研究報告推薦方案的線路走向和主要控制點,確定 採用國家統一3°帶高斯平面直角坐標系,觀測結果歸算至參考橢球面上(適用條件),並擬出計算簡便、精度可靠的調整放線距離公式及其計算方案(初步設計中再予核實),交由施工人員實施。
依據長度綜合變形公式⑸及它的說明,當坐標反算距離d=1000 m,每公里地面實際長度減去坐標反算距離:
 允差分析法
允差分析法見右圖。
式中, d坐標反算距離,單位為 m; H 縱斷面設計高程,單位為 m, B 檢查點高程對變形影響值,單位為 mm/km; ym 檢查點距中央子午線距離,單位為 km; C 檢查點距中央子午線距離對變形影響值,單位為 mm/km;係數 F=坐標反算距離/1000,移動 d的小數點位置,保留兩位小數。特彆強調,隧道的開挖、放線都是在洞內縱斷面設計高程面上進行的,只有保證這個面的精度才有意義。若採用洞頂、溝底地面高程的平均值來取代它則不合理。
誤差分析
C值的變化以不超過一定的限差沿某一確定常數上下浮動,可取中數簡化,取代各檢查點計算的C值,簡化值與用公式計算值之差即本項誤差。總長超過1000m的橋隧和特殊的橋樑誤差宜控制在6mm以內,一般工程宜控制在21mm以內。
B同理,在縱斷面每公里+500處讀、記設計高程H,作為本公里的常數代入公式計算。多數工程縱坡小於5%,H誤差最大25m,B值誤差最大為4mm。
按以上誤差分析,即便是同地點、同符號最不利的組合,總誤差也不會大於規範規定的限差。
通過上述分析,建立調整放線距離公式:
 允差分析法
允差分析法見右圖。
這種 用誤差分析削弱投影變形以滿足允許限差要求的方法稱之為“ 允差分析法”或“ 調整距離法”。並將公式(21)命名為“允差分析法削弱變形調距公式”,簡稱“調距公式”。
 允差分析法
允差分析法算例可參照論文,見參考文獻。