定義
英文名:Series of Preferred Numbers。
優先數: 優先數由公比分別為10的5、10、20、40、80次方根,且項值中含有10的整數冪的理論等比數列導出的一組近似等比的數列。
各數列分別用符號 R5、R10、R20、R40和R80表示,稱為R5係數、R10係數、R20係數、R40係數和R80係數。
基本系列表和 補充系列R80表中列出的1~10這個範圍與其一致,這個優先數系可向兩個方向無限延伸,表中值乘以10的正整數冪或負整數冪後即可得其他十進制項值。
優先數系中任一個項值均稱為優先數。
優先數系是國際上統一的數值分級制度。我國的國家標準為GB/T 321-2005,國際標準為ISO3、ISO17、ISO497。
優先數系有很多優點,工程技術上的各種參數指標,特別是需要分檔分級的參數指標,採用優先數系可以防止數值傳播的紊亂。
優先數系不僅適用於標準的制訂,而且適用於標準制訂以前的規劃、設計階段,從而把產品品種的發展,從一開始就引導到合理的標準化的軌道上。
優先數系由一些十進制等比數列構成,數列的簡號為Rr 。
優先數
按國家標準GB/T 321-2005 《優先數和優先數系》的定義。
優先數:符合R5、R10、R20、R40和R80系列的圓整值。
其具體數值為:
R5系列
1.00 1.60 2.50 4.00 6.30 10.00
R10系列
1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00 10.00
R20系列
1.00 1.12 1.25 1.40 1.60 1.80 2.00 2.24 2.50 2.80 3.15 3.55 4.00 4.50 5.00 5.60 6.30 7.10 8.00 9.00 10.00
R40系列
1.00 1.06 1.12 1.18 1.25 1.32 1.40 1.50 1.60 1.70 1.80 1.90 2.00 2.12 2.24 2.36 2.50 2.65 2.80 3.00 3.15 3.35 3.55 3.75 4.00 4.25 4.50 4.75 5.00 5.30 5.60 6.00 6.30 6.70 7.10 7.50 8.00 8.50 9.00 9.50 10.00
R80系列
1.00 1.03 1.06 1.09 1.12 1.15 1.18 1.22 1.25 1.28 1.32 1.36 1.40 1.45 1.50 1.55 1.60 1.65 1.70 1.75 1.80 1.85 1.90 1.95 2.00 2.06 2.12 2.18 2.24 2.30 2.35 2.43 2.50 2.58 2.65 2.72 2.80 2.90 3.00 3.07 3.15 3.25 3.35 3.45 3.55 3.65 3.75 3.85 4.00 4.12 4.25 4.37 4.50 4.62 4.75 4.87 5.00 5.15 5.30 5.45 5.60 5.80 6.00 6.15 6.30 6.50 6.70 6.90 7.10 7.30 7.50 7.75 8.00 8.25 8.50 8.75 9.00 9.25 9.50 9.75 10.00
優先數的由來
十九世紀末,法國的法國人查爾斯·雷諾(Charles Renard) 為了對氣球上使用的繩索規格進行簡化,做出這樣的規定,簡化後形成的尺寸規格系列,每進5項值增大10倍(十進幾何級數)。
其它相關術語
1.優先數Perferred Numbers
符合R5、R10、R20、R40和R80系列的圓整值。
2.基本系列Basic Series
R5、R10、R20和R40四個系列是優先數系中的常用系列。
注1 基本系列中的優先數常用值,對計算值的相對誤差在+1.26%~1.01%範圍內。
R5 ≈1.60
R10≈1.25
R20≈1.12
R40≈1.06
3.系列代號Designation of Series
優先數的所有系列均以字母R為符號開始。
4.序號Serial Numbers
表明優先數排列次序的一個等差數列,它從優先數1.00的序號0開始計算。
5.計算值Calculated Values
對理論值取五位有效數字的近似值,計算值對理論值的相對誤差小於1/20000。
註:在作參數系列的精確計算時可用來代替理論值。
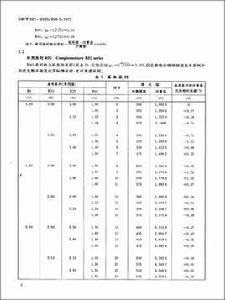
6.補充系列R80 Complementary R80 Series
R80系列稱為補充的系列,它的公比大約等於1.03,僅在參數分級很細或基本系列中的優先數不能適應實際情況時,才可考慮採用。
7.派生系列
派生系列是從基本系列或補充系列R中每p項取值導出的系列,以Rr/p表示,比值r/P是1-10、10-100。等各個十進制數內項值的分級數。
派生系列的公比為10的r次方根的p次方。
8.一般情況
設:r是基本系列的指數,r=5、10、20或40。
P是派生系列的間距,即組成派生系列時,在基本系列中所要求的間隔項數。
派生系列公比是10的r次方根的p次方。
9.理論值Theoretical Value
10的5、10等次方根的N次方理論等比數列的連續項值,其中N為任意整數。
註:理論值一般是無理數,不便於實際套用 。
要點和原則
1.在確定產品的參數或參數系列時,如果沒有特殊原因而必須選用其他數值的話,只要能滿足技術經濟上的要求,就應當力求選用優先數,並且按照R5、R10、R20和R40的順序,優先用公比較大的基本系列;當一個產品的所有特性參數不可能都採用優先數,也應使一個或幾個主要參數採用優先數;即使單個參數值,也應按上述順序選用優先數。這樣做既可在產品發展時插入中間值仍保持或逐步發展成為有規律的系列,有便於跟其它相關產品協調配套。
2.當基本系列的公比不能滿足分級要求時,可選用派生系列。選用時應優先採用公比較大和延伸項中含有項值1的派生系列。移位系列只宜用於因變數參數的系列。
3.當參數系列的延伸範圍很大,從製造和使用的經濟性考慮,在不同的參數區間,需要採用公比不同的系列時,可分段選用最適宜的基本系列或派生系列,以構成複合系列。
4.按優先數常用值分級的參數系列,公比是不均等的。在特殊情況下,為了獲得公比精確相等的系列,可採用計算值。
5.如無特殊原因,應儘量避免使用化整值。因為化整值的選用帶有任意性,不易取得協調統一,而且由於誤差較大帶來一些缺點。如系列中含有化整值,就使以後向較小公比的系列轉換變得較為困難,化整值系列公比的均勻性差,化整值的相對誤差經乘,除運算後往往進一步增大等等 。
優點
1、經濟合理的數值分級制度產品的參數從最小到最大有很寬的數值範圍,經驗和統計表明,數值按等比數列分級,能在較寬的範圍內以較少的規格,經濟合理地滿足社會需要。這就要求用“相對差”反映同樣“質”的差別,而不能象等差數列那樣只考慮“絕對差”。例如,對軸徑分級,在10mm不合需要時,如用12mm,則兩極之間絕對差為2mm,相對差為20%。但對100mm來說,加大2mm變成102mm,相對差只有2%,顯然太小。而對直徑為1mm的軸來說,加大2mm變成3mm,相對差200%顯然太大。等比數列是一種相對差不變的數列,不會造成分級疏的過疏,密的過密的不合理現象,優先數系正是按等比數列制訂的。因此,它提供了一種經濟,合理的數值分級制度。
2、統一、簡化的基礎
一種產品(或零件)往往同時在不同的場合,由不同的人員在分別進行設計和製造,而產品的參數又常常影響到與其有配套關係的一系列產品有關參數。如果沒有一個共同遵守的選用數據的準則,勢必造成同一種產品的尺寸參數雜亂無章,品種規格過於繁多。優先數系是國際上統一的數值制度,可用於各種量值的分級,以便在不同的地方都能優先選用同樣的數值,這就為技術經濟工作上統一,簡化和產品參數的協調提供了基礎。
按優先數系確定的參數和系列,在以後的標準化過程中(從企標發展到行標、國標等),有可能保持不變,這在技術上和經濟上都有很大意義。
企業自製自用的工藝裝備等設備的參數,也應當選用優先數系。這樣,不但可簡化,統一品種規格,而且可使尚未標準化的對象,從一開始就為走向標準化奠定了基礎。
在制訂標準或規定各種參數的協商中,優先數系應當成為用戶和製造廠之間或各有關單位之間的共同遵循的準則,以便在無偏見的基礎上達到一致。
3、具有廣泛的適應性
優先數中包含有各種不同公比的系列,因而可以滿足較密和較疏的分級要求。由於較疏系列的項值包含在較密的系列只中,這樣在必要時可插入中間值,使較疏的系列變成較密的系列,而原來的項值保持不變,與其他產品間配套協調關係不受影響,這對發展產品品種是很順利的。
在參數範圍很寬時,根據情況可分段選用最合適的基本系列,以複合系列的形式來組成最佳系列。
由於優先數的積或商仍為優先數,這就更進一步擴大了優先的適用範圍。例如,當直徑採用優先數。於是圓周速度、切線速度,圓柱體的面積和體積,球的面積和體積等也都是優先數。
優先數系適用於能用數值表示的各種量值的分級,特別是產品的參數系列。如長度、直徑、面積、體積、載荷、應力、速度、時間、功率、電流、電壓、流量、濃度、傳動比、公差、測量範圍、試驗或檢驗工作中測點的間隔以及無量綱的比例係數等。凡在取值上具有一定自由度的參數系列,都應最大限度地選用優先數,不僅在制訂產品標準時,特別在產品設計中應當有意識地使主要尺寸,參數符合優先數。
4、簡單、易記、計算方便
優先數系是十進等比數列,其中包含10的所有整數冪。只要記住一個十進段內的數值,其他的十進段內的數值可由小數點的移位得到。所以只要記住R20中的21個數值,就可解決一般套用。
優先數系是等比數列,故任意個優先數的積和商仍為優先數,而優先數的對數(或序號)則是等差數列,利用這些特點可以大大簡化設計計算 。