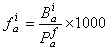偶極子流

偶極子流，等強度源流和匯流的一種組合，其中點源和點匯無限接近並保持強度和距離的乘積等於一常數值。設O點和O┡點上分別有強度均為Q的點匯和點源,它們對空間中任一點P所感生的速度勢。

偶極子流

正文

ф為：

,

式中r和r┡分別為O和O┡到P的距離。令O┡趨於O,並要求Q·OO┡→m，得偶極子速度勢的表達式：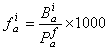

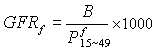式中為函式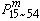在L方向上的方嚮導數；θ為L和OP的夾角；m為偶極矩矢量，其大小為m，方向由匯到源，可見偶極子有方向性。從匯向源引出的直線是偶極子的軸線。取球坐標系，使方程中的θ和球坐標系中的坐標θ重合。根據軸對稱性，存在著流函式Ψ，使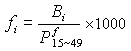

式中vr、vθ為r、θ方向的速度分量，積分之，得：

，

這裡約定θ＝0時Ψ＝0。在柱坐標系中，偶極子的ф和Ψ的表達式為：

。

對平面偶極子進行完全類似的定義和討論，可得ф和Ψ的表達式： 它的復變解析函式（即復位勢）的表達式為： 式中,β為OL與x軸的夾角（圖1）。偶極子流的流線族和等勢線族如圖2、圖3所示，它們顯然是正交的。在二維偶極子流中，流線是圓心在y軸上的圓，而等勢線則為圓心在x軸上的圓（圖2）。在三維偶極子流中，等勢線和流線組成的正交曲線網和二維情形相似,但它們的形狀已經不是圓了（圖3）。

偶極子流是一種重要的基本流子，它和其他基本流子疊加在一起，可以得到一些很典型的流動。例如均勻流同一個方向與均勻流相反的平面偶極子疊加，得到均勻來流繞圓柱的流動；均勻流同一個方向與均勻流相反的三維偶極子疊加，則得均勻來流繞圓球的流動(圖)，其速度勢ф的方程為：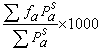

，

式中V∞為均勻來流的速度；α為圓球半徑；r、θ為球極坐標。和三維點源一樣，三維偶極子也可以連續地分布在曲線、曲面或體積內，使單位長度、單位面積或單位體積上的強度保持有限，從而為解決繞流問題提供另一類奇點組合。例如，沿圓周均勻分布偶極子強度，使偶極子軸線與圓周所在的平面垂直，再在偶極子的負軸方向疊加一均勻流動，就可得到繞圓環形物體的流動。

配圖

相關連線