偏態

偏態（skewness）是指非對稱分布的偏斜狀態。換句話說，就是指統計總體當中的變數值分別落在眾數（M0）的左右兩邊，呈非對稱性分布。偏態於1895年由統計學家皮爾遜（K.Pearson）首次提出，是對數據分布對稱性的測度。測度偏態的統計量是偏態係數（coefficient of skewness），記作SK。

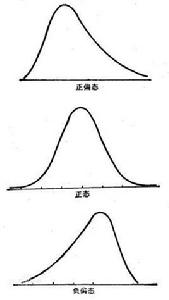
偏態

定義

為統計學概念，即統計數據峰值與平均值不相等的頻率分布。根據峰值小於或大於平均值可分為正偏函式和負偏函式，其偏離的程度可用偏態係數刻畫。

種類

在統計學上，眾數和平均數之差可作為分配偏態(skewnessdistribution)的指標之一。如平均數大於眾數，稱為正偏態(positiveskewness)；相反，則稱為負偏態(negativeskewness)。即：

如果X'>M0，這種偏態稱為正偏態或右偏態，正偏態g1>0；

如果X'<M0，這種偏態稱為負偏態或左偏態，負偏態g1<0 。（左右偏態修正，20171116）

偏態係數測定法

主要有皮爾遜偏態係數測定法和中心距偏態係數測定法兩種。

在spss的Descriptives描述中有峰度係數和偏度係數， Sk=0，Ku=3時，分布呈正態，Sk>0時，分布呈正偏態，Sk<0時，分布呈負偏態，Ku>3時曲線比較陡峭，Ku<3時曲線比較平坦。由此可判斷本數據分布是否為常態分配。

特點

與常態分配相對而言，偏態分布有兩個特點：

一是左右不對稱（即所謂偏態）；

二是當樣本增大時，其均數趨向常態分配。