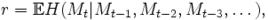定量定義
在描述原始數據的冗餘時,信源信息率為平均每個符號的熵。對於無記憶信源,這僅是每個符號的熵;而對於一個隨機過程的最普遍形式為前 n個符號的聯合熵除以 n之後,隨著 n趨於無窮時的極限
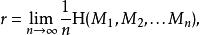 信息冗餘
信息冗餘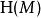 信息冗餘
信息冗餘在資訊理論中經常提及一種語言的“熵率”或者“信息熵”。當信源是英文散文時這是正確的。由於無記憶信源的訊息之間沒有相互依賴性,所以無記憶信源的信息率為 。
信源的 絕對信息率為
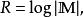 信息冗餘
信息冗餘即是訊息空間基數的對數值。這個公式也稱作Hartley函式。這是傳送用這個字母表表示的信息的最大信息率。其中對數要根據所用的測量單位選擇合適的底數。若且唯若信源是無記憶的且均勻分布的時候,絕對信息率等於信息率。
絕對信息冗餘定義為
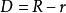 信息冗餘
信息冗餘即信息率與絕對信息率之間的差。
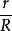 信息冗餘
信息冗餘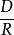 信息冗餘
信息冗餘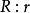 信息冗餘
信息冗餘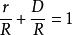 信息冗餘
信息冗餘稱為 相對信息冗餘,它表示了最大的數據壓縮率,這個壓縮率用檔案大小減小比例所表示。當用原始檔案與壓縮後的檔案表示的時候, 表示能夠得到的最大壓縮率。與相對信息冗餘互補的是 效率 ,於是 。均勻分布的無記憶信源的冗餘為0,效率為100%,因此無法壓縮。
其它的冗餘概念
兩個變數之間 冗餘的度量是互信息或者正規化變數。多個變數之間冗餘的度量是全相關(total correlation)。
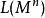 信息冗餘
信息冗餘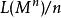 信息冗餘
信息冗餘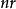 信息冗餘
信息冗餘 信息冗餘
信息冗餘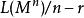 信息冗餘
信息冗餘 信息冗餘
信息冗餘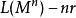 信息冗餘
信息冗餘壓縮數據的冗餘是指 n}個訊息的期望壓縮數據長度為(或期望數據熵率)與熵值(或熵率)的差。(這裡我們假設數據是遍歷的也是平穩的,例如無記憶信源。)雖然熵率之差會隨著增加而任意小,實際的差已不能(儘管理論上可以)在有限熵的無記憶信源情況下上界為 1。