定義
 保守矢量場
保守矢量場 保守矢量場
保守矢量場一個矢量場 稱為 保守的 ,如果存在一個標量場 ,使得:
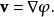 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場在這裡, 表示 的梯度。當以上的等式成立時, 就稱為 的一個標量勢。
矢量分析基本定理表明,任何一個矢量場都可以表示為一個保守矢量場和一個螺線矢量場的和。
路徑無關
 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場保守矢量場的一個重要性質是它沿著一條路徑的積分只與起點和終點有關,與路徑無關。假設 是三維空間內的一個區域, 是 內的一個可求長路徑,其起點為 ,終點為 。如果 是保守矢量場,那么:
 保守矢量場
保守矢量場這是複合函式求導法則和微積分基本定理的結果。
 保守矢量場
保守矢量場一個等價的表述是,對於 內的所有閉合路徑,都有:
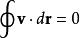 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場以上的逆命題也是成立的,只要 是連通區域。也就是說,如果 沿著 內的所有閉合路徑的環量都是零,那么 就是保守矢量場。
保守力
如果力的矢量場是保守的,則這個力稱為保守力。
 保守矢量場
保守矢量場 保守矢量場
保守矢量場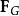 保守矢量場
保守矢量場最明顯的例子是萬有引力。根據牛頓萬有引力定律,兩個質點 和 之間的引力 等於:
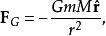 保守矢量場
保守矢量場 保守矢量場
保守矢量場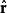 保守矢量場
保守矢量場 保守矢量場
保守矢量場 保守矢量場
保守矢量場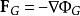 保守矢量場
保守矢量場其中 是引力常數, 是單位矢量,從 指向 。萬有引力是保守的,這是因為 ,其中
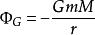 保守矢量場
保守矢量場是引力勢。
 保守矢量場
保守矢量場 保守矢量場
保守矢量場對於保守力, 路徑無關可以解釋為從點 到點 所做的功是與路徑無關的,沿著閉合路徑所做的功是零:
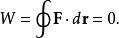 保守矢量場
保守矢量場
