保守場

如果一個矢量場是某個標量勢的梯度，那么便稱為保守場。一個矢量場V 稱為保守的，即如果存在一個標量場φ，使得V=▽φ。在這裡▽φ表示φ的梯度。當以上的等式成立時，φ就稱為V的一個標量勢。保守場的第二類曲線積分只於起點和終點有關，而與路徑無關。任何一個保守場的 鏇度都是零（因此是無鏇的），也具有路徑無關的性質。矢量分析基本定理表明，任何一個矢量場都可以表示為一個保守矢量場和一個螺線矢量場的和。

性質

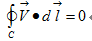保守場性質

保守場的第二類曲線積分只於起點和終點有關，而與路徑無關。

這也是判定保守場的方法。

跟物體在重力場中移動過程中重力做功一樣，電荷在電場中移動時電場力做功．電荷在靜電場中從一點移到另一點時，電場力的功的值只跟始末兩點的位置有關，而和所經過的路徑的形狀完全無關．如果電荷在靜電場中的某點出發沿任意閉合路徑又回到原出發點(即始末兩點，在同一位置)，電場力所做的功等於零．具備這種特點的力和場稱為保守力和保守場．靜電場力和重力都是保守力，靜電場和重力場是保守場．

解析

有兩個密切相關的概念：

路徑無關和

無鏇矢量場。任何一個保守場的 鏇度都是零（因此是無鏇的），也具有路徑無關的性質。矢量分析基本定理表明，任何一個矢量場都可以表示為一個保守矢量場和一個螺線矢量場的和。