套用
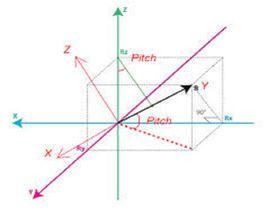
作用量-角度坐標主要用於完全可分的哈密頓-亞可比方程(哈密頓量顯性地不含時間,也就是說,能量保持恆定)。 作用量-角度變數可以用來定義一個環面不變數。因為,保持作用量的不變設定了環的曲面,而角度是環面的另外一個坐標,粒子依照著角度,卷繞於環面。
在量子力學早期,波動力學發展成功之前,玻爾-索末菲量子化條件(Bohr-Sommerfeld quantization) 是研究量子力學的利器。此條件闡明,作用量必須是普朗克常數常數的整數倍。愛因斯坦對於Einstein-Brillouin-Keller action quantization深刻的理解 與 非可積分系統 量子化的困難,都是以 作用量-角度坐標的環面不變數 來表達。
在哈密頓力學裡,作用量-角度坐標也可以套用於攝動理論,特別是在決定緩漸不變數。關於一個自由度很小的動力系統的非線形攝動,混沌理論研究的最早的一個結果是KAM theorem。這定理闡明,對於微小攝動,環面不變數是穩定的。
作用量-角度坐標,對於戶田晶格(Toda field theory) 的解析,對於Lax pairs的定義,更廣義地,對於一個系統同光譜(isospectral) 演化的構想,都占有關鍵地位。
周期性運動的坐標表示
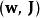 作用量-角度坐標
作用量-角度坐標假若,粒子的運動是周期性運動,最常見的例子如振動或旋轉都是周期性運動,則可以設計一個新正則坐標-作用量-角度坐標 。定義作用量為
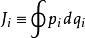 作用量-角度坐標
作用量-角度坐標這閉路徑積分的路徑是粒子運動一周期的路徑。
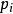 作用量-角度坐標
作用量-角度坐標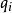 作用量-角度坐標
作用量-角度坐標 作用量-角度坐標
作用量-角度坐標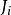 作用量-角度坐標
作用量-角度坐標 作用量-角度坐標
作用量-角度坐標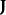 作用量-角度坐標
作用量-角度坐標由於廣義動量 只跟 、 有關,經過積分,作用量 只跟 有關。所以,作用量矢量 只是個常數矢量。哈密頓特徵函式可以表達為
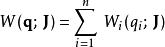 作用量-角度坐標
作用量-角度坐標雖然是同樣的物理量,函式的參數不同,形式也不同。
 作用量-角度坐標
作用量-角度坐標定義角度 為
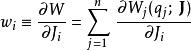 作用量-角度坐標
作用量-角度坐標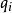 作用量-角度坐標
作用量-角度坐標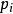 作用量-角度坐標
作用量-角度坐標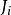 作用量-角度坐標
作用量-角度坐標由於所有的廣義坐標 都相互獨立,所有的廣義動量 也都相互獨立,所以,所有的作用量 都相互獨立,作用量-角度坐標可以正確的用為正則坐標。這樣,哈密頓特徵函式可以用正則坐標作用量-角度坐標表達為
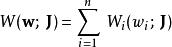 作用量-角度坐標
作用量-角度坐標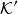 作用量-角度坐標
作用量-角度坐標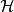 作用量-角度坐標
作用量-角度坐標新哈密頓量 與舊哈密頓量 相等:
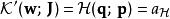 作用量-角度坐標
作用量-角度坐標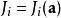 作用量-角度坐標
作用量-角度坐標因為作用量只是常數矢量,所以,
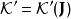 作用量-角度坐標
作用量-角度坐標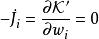 作用量-角度坐標
作用量-角度坐標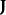 作用量-角度坐標
作用量-角度坐標 作用量-角度坐標
作用量-角度坐標新哈密頓量,只跟作用量 有關,跟角度無關。
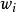 作用量-角度坐標
作用量-角度坐標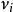 作用量-角度坐標
作用量-角度坐標角度隨時間的導數,可以用哈密頓方程決定:
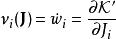 作用量-角度坐標
作用量-角度坐標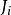 作用量-角度坐標
作用量-角度坐標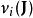 作用量-角度坐標
作用量-角度坐標每一個 都是常數,所以,也是常數:
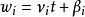 作用量-角度坐標
作用量-角度坐標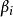 作用量-角度坐標
作用量-角度坐標其中,是積分常數。
基本規則總結
一般程式有三個步驟:
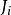 作用量-角度坐標
作用量-角度坐標1)計算作用量變數。
2)用作用量變數表示原本哈密頓量。
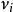 作用量-角度坐標
作用量-角度坐標3)取哈密頓量關於作用量變數的導數。這樣,可以求得頻率 。