歷史
馬克斯·普朗克對於光波的發射和吸收的研究,點燃了舊量子論。後來,愛因斯坦發表了固體比熱的傑作。緊接著,套用量子原理於原子運動,彼得·德拜解釋了比熱的異常現象。這些貢獻開啟了舊量子論如火如荼的發展。
1913年,玻爾發表了對應原理。套用這原理,他又建構了氫原子的玻爾模型,成功地解釋出氫原子的發射譜線。
整個1910年代,一直到1920年代中期,物理學家套用舊量子論為一個解析原子問題的嶄新利器。但是有成功也有失敗,效果並不一致。在這期間,科學家知曉了分子的旋轉和振動譜線,也發現了電子自旋;但這些也引起了半整數量子數的困惑。愛因斯坦提出了零點能量理論。阿諾·索末菲半經典地量子化相對論性氫原子。克拉莫給予了斯塔克效應(Stark effect)一個合理的解釋。薩特延德拉·玻色和愛因斯坦正確地找到了光子的量子統計。
於1924年,克拉莫發表了量子色散理論,借著運動軌道的傅立葉分量,可以計算從一個量子態躍遷至另一個量子態的機率。通過與海森堡的合作,這點子被延伸為一個半經典的,以類似矩陣的形式來描述的原子躍遷機率。海森堡繼續這研究,以這躍遷方法來重新表述量子理論,原創出矩陣力學。
同樣於1924年,德布羅意提出物質的波動理論。在1926年,薛丁格找到了一個量子波動方程,能夠清楚明了,前後一致地複製舊量子論的所有成果。後來,薛丁格證明了他的波動力學和海森堡矩陣力學是等價的。波動力學和矩陣力學共同結束了舊量子論的時代。
緒論
舊量子論是一些比現代量子力學還早期,出現於1900年至1925年之間的量子理論。雖然並不很完整或一致,這些啟發式理論是對於經典力學所做的最初始的量子修正。舊量子論最亮麗輝煌的貢獻無疑應屬玻爾模型。自從夫朗和斐於1814年發現了太陽光譜的譜線之後,經過近百年的努力,物理學家仍舊無法找到一個合理的解釋。而玻爾的模型居然能以簡單的算術公式,準確地計算出氫原子的譜線。這驚人的結果給予了科學家無比的鼓勵和振奮,他們的確是朝著正確的方向前進。很多年輕有為的物理學家,都開始研究量子方面的物理。因為,可以得到很多珍貴的結果。
直到今天,舊量子論仍舊有聲有色地存在著。它已經轉變成一種半經典近似方法,稱為WKB近似。許多物理學家時常會使用WKB近似來解析一些極困難的量子問題。在1970年代和1980年代,物理學家Martin Gutzwiller發現了怎樣半經典地解析混沌理論之後,這研究領域又變得非常熱門。
基本原理
舊量子論的基本原理談到原子系統的運動是量子化的,離散的。原子系統遵守經典力學;但不是每一種運動都合法,只有那些遵守 舊量子條件的運動是合法的:
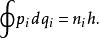 舊量子論
舊量子論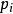 舊量子論
舊量子論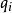 舊量子論
舊量子論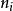 舊量子論
舊量子論其中, 是動量, 是對應的坐標, 是整數的量子數,h是普朗克常數。
舊量子條件又稱為 威耳遜-索末菲量子化定則,是由威耳遜和索末菲各自發現的。舊量子條件公式的閉路積分取於整個運動的一周期,是相空間的面積,稱為作用量。由於在這裡,作用量被量子化為以普朗克常數為單位的整數,因此,普朗克常數時常被稱為 作用量的量子。
為了要符合舊量子條件,經典運動必須是可分的,意思是說,運動方程可以分為幾個獨立部分,每一個獨立部分都包含了一個不同的坐標,而每一個坐標的方程部分所描述的運動都是周期性的。不同部分描述的運動不一定會有同樣的周期,它們的周期甚至是互相不可通約的。可是,整個系統必須有一組可分的坐標,每一個坐標的方程部分都分別描述一個周期性的運動。
使用舊量子條件的動機,一個是對應原理,還有一個就是量子化的物理量必須是緩漸不變數的實際物理觀察。例如,給予諧振子的普朗克量子化定律,這兩個條件中,任意一個條件決定了量子化一個一般系統的正確經典物理量。
範例
一維位勢
一維問題的解析相當容易。給予任意能量E,從能量守恆定律,可以計算出粒子的動量:
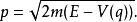 舊量子論
舊量子論其中,V(q)是坐標為q的地點的位勢。
轉向點是粒子動量消失的位置。在經典轉向點之間,將這動量的公式積分於所有q的可能值,再加入舊量子條件,就可以得到舊量子條件的方程。
假設,這問題是盒中粒子問題。則舊量子條件方程為
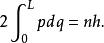 舊量子論
舊量子論其中,n是正整數,L是盒子的長度。
那么,容許的動量是
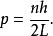 舊量子論
舊量子論容許的離散能級是
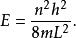 舊量子論
舊量子論旋轉子
在一根長度為 R的無質量剛桿的一端,連結著一個質量為M的粒子,稱這連結體為 旋轉子。假設,剛桿的另外一端固定於一個固定點,則旋轉子可以繞著這固定點作旋轉運動。採用極坐標系,這旋轉子的旋轉運動的拉格朗日量L是
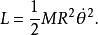 舊量子論
舊量子論 舊量子論
舊量子論其中,是角坐標。
角坐標的共軛動量J是
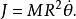 舊量子論
舊量子論 舊量子論
舊量子論舊量子條件要求的周期、J,兩個物理量的乘積為普朗克常數乘以整數倍數n:
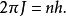 舊量子論
舊量子論也就是說,角動量J是約化普朗克常數的整數倍數。將這舊量子條件帶入玻爾模型,就可以得到氫原子的能級!
氫原子
氫原子物理的角部分只是一個旋轉子,給出量子數l、m。剩餘的徑向部分是在位勢作用下的周期性一維運動,可以解析。
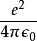 舊量子論
舊量子論給予固定值的總角動量L,一個經典克卜勒問題的哈密頓量H是(為了簡化方程,重定義質量的單位和能量的單位。這樣,可以吸收兩個常數:質量和庫侖定律的係數):
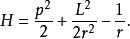 舊量子論
舊量子論其中,r是徑向坐標,p是徑向動量。
設定能量為常數E,徑向動量是
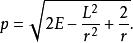 舊量子論
舊量子論由於位勢乃反平方連心勢,經典的電子運動軌道是橢圓。近拱點和遠拱點分別是當p=0時電子位置的徑向坐標:
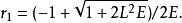 舊量子論
舊量子論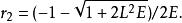 舊量子論
舊量子論所以,舊量子條件是
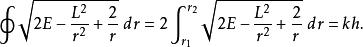 舊量子論
舊量子論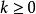 舊量子論
舊量子論其中,是一個新的量子數。
經過一番運算,可以得到
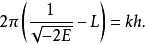 舊量子論
舊量子論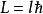 舊量子論
舊量子論將量子化的角動量代入,稍加編排,可得能量為
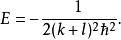 舊量子論
舊量子論兩個量子數k、l共同決定了能量。設定主量子數n:n=k+l。由於k是非負整數, l的容許值必須小於或等於n。除了某些小地方以外,這結果與玻爾模型的能級結果完全相同。
前述關於氫原子的半經典理論稱為 索末菲模型。其軌道是各種不同尺寸的橢圓軌道處於離散的傾斜平面。索末菲模型預測,原子沿著某直軸的磁矩,只能給出離散值。這預測似乎與旋轉不變性相矛盾,但是卻被施特恩-格拉赫實驗證實是正確的。
克拉莫躍遷關係
舊量子論只能適用於特定的力學系統,能夠用周期性的作用量-角度變數來分離的特別力學系統。舊量子論無法處理輻射的發射和吸收。雖然這樣,亨德里克·克拉莫(Hendrik Kramers)找到了一個啟發式,描述怎樣計算輻射的發射和吸收。
克拉莫建議,應該傅立葉分析一個量子系統的軌道,將軌道依照軌道頻率的倍數分解成調和函式:
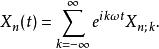 舊量子論
舊量子論 舊量子論
舊量子論其中,下標n是軌道的量子數,在索末菲模型里,代表n,l,m量子數組,是軌道的角頻率,k是傅立葉模態。
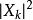 舊量子論
舊量子論克拉莫注意到,只有當頻率是軌道頻率的整數倍數的時候,才會發生輻射的經典發射。在他的量子色散理論里,他提議兩個物理態之間的躍遷可以比擬為輻射的經典發射。那么,輻射的發射率應正比於,如同在經典力學的應有的物理行為。克拉莫的描述並不精確,因為傅立葉分量的頻率並不完全匹配能級之間的差距。這點子後來引導出矩陣力學的發展。

