定義與概念
假設隨機變數X為等到第α件事發生所需之等候時間, 密度函式為
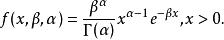 伽馬分布
伽馬分布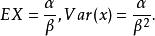 伽馬分布
伽馬分布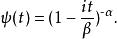 伽馬分布
伽馬分布特徵函式為
均值與方差
伽馬分布的均值與方差分別為
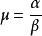 伽馬分布
伽馬分布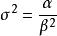 伽馬分布
伽馬分布變化趨勢
 伽馬分布
伽馬分布伽馬分布的機率密度函式和失效率函式取決於形狀參數的數值。
 伽馬分布
伽馬分布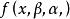 伽馬分布
伽馬分布當時,為遞減函式;
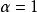 伽馬分布
伽馬分布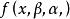 伽馬分布
伽馬分布當時,為遞增函式;
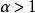 伽馬分布
伽馬分布 伽馬分布
伽馬分布當時,為單峰函式;
伽馬分布的特性
Gamma的可加性
兩個獨立隨機變數X和Y,且X~Ga(a,γ),Y~Ga(b,γ),則Z = X+Y ~ Ga(a+b,γ)。注意X和Y的尺度參數必須一樣。
數學表達式
若隨機變數X具有機率密度
其中α>0,β>0,則稱隨機變數X服從參數α,β的伽馬分布,記作G(α,β).
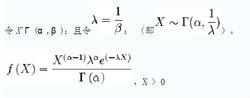 伽馬分布
伽馬分布Gamma分布的特殊形式
當形狀參數α=1時,伽馬分布就是參數為γ的指數分布,X~Exp(γ)
當α=n/2,β=1/2時,伽馬分布就是自由度為n的卡方分布,X^2(n)

