定義
數學上對如下形式常微分方程解函式序列：
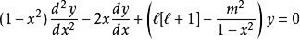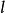伴隨勒讓德多項式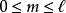
伴隨勒讓德多項式
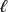伴隨勒讓德多項式
伴隨勒讓德多項式
伴隨勒讓德多項式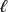 伴隨勒讓德多項式 伴隨勒讓德多項式 伴隨勒讓德多項式該方程是在球坐標系下求解拉普拉斯方程時得到的，因上述方程僅當 和 均為整數且滿足 時，才在區間 [−1, 1] 上有非奇異解，所以通常把 和 均為整數時方程的解稱為 伴隨勒讓德多項式；把 和 為一般實數或複數時方程的解稱為廣義勒讓德函式（generalized Legendre functions）。
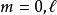伴隨勒讓德多項式當 為整數時，方程的解即為一般的 勒讓德多項式。
注意當 m 為奇數時，連帶勒讓德多項式並不是多項式。
正交性
與勒讓德多項式一樣，伴隨勒讓德多項式在區間 [-1,1] 上也滿足正交性。
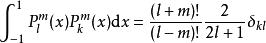伴隨勒讓德多項式這是因為，與勒讓德方程一樣，伴隨勒讓德方程也是施圖姆-劉維爾型的：
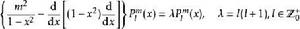伴隨勒讓德多項式正交性的另一種表述如下，它與下面提到的球諧函式有關。
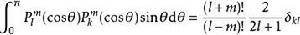伴隨勒讓德多項式與勒讓德多項式的關係
伴隨勒讓德多項式可以由勒讓德多項式求m次導得到：
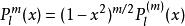伴隨勒讓德多項式等號右邊的上標 (m) 表示求m次導。
與超幾何函式的關係
伴隨勒讓德函式（即 l, m 不一定要是整數）可以用高斯超幾何函式表達為：
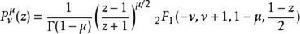伴隨勒讓德多項式注意 μ 為正整數 m 時 1-μ 是伽瑪函式的奇點，此時等號右邊的式子應該理解為當 μ 趨於 m 時的極限。
負數階連帶勒讓德多項式
顯然伴隨勒讓德方程在變換m→-m下保持不變，傳統上習慣定義負數階伴隨勒讓德多項式為：
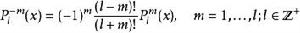伴隨勒讓德多項式容易驗證，這樣定義的伴隨勒讓德多項式能夠使得上面的正交關係可以推廣到 m 為負數的情況。
注意在個別文獻（如圖1）中會直接取
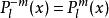伴隨勒讓德多項式
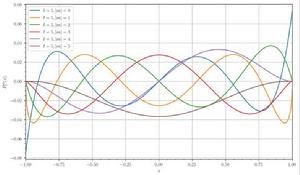圖1 l=5時連帶勒讓德多項式的圖像與球諧函式的關係
球諧函式是球坐標下三維空間拉普拉斯方程的角度部分的解，構成一組完備的基組，有著重要的意義。採用本文中定義的伴隨勒讓德多項式的表達式，球諧函式可以表達為：
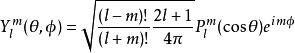伴隨勒讓德多項式由伴隨勒讓德多項式的正交關係可以直接得到球諧函式的正交關係：
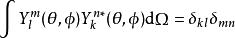伴隨勒讓德多項式式中 dΩ 是立體角元。
