企業庫存模型
正文
輔助企業管理人員確定計畫期內企業生產所需物資的合理訂貨批量、訂貨點和訂貨間隔時間的模型。其目的是在保證正常生產的條件下使庫存總費用最少。庫存模型分為兩大類型。①確定型庫存模型：指需求和訂貨數量均為確定的庫存模型，又可進一步按允許缺貨和不允許缺貨,計算或不計算補充貨物所需時間,有無約束條件，以及需求數量與供應價格有無關係等進行分類。②隨機型庫存模型：又可分為需求量是隨機的，訂貨供應時間為確定的；需求量和訂貨供應時間均為隨機的；以及其他多種類型。經濟訂貨批量模型
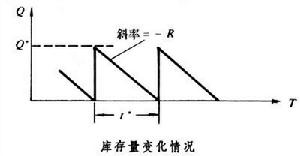
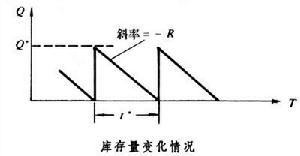經濟訂貨批量模型是確定型庫存模型的一種。它是在以下條件下建立的：①需求是連續的、均勻的，需求速度 R（即單位時間需求量）是一常數。②不允許缺貨，即缺貨時其賠償費用假定為無窮大。③當庫存量降至零時可立即得到補充，即訂貨周期可以近似地看作為零（庫存量變動情況可用下圖表示）。④每批訂貨量 Rt及訂貨費用kRt不變（k為單位物資價格）。每批訂貨手續費 C3不變。⑤單位物資平均庫存費用 C1不變。根據上述5條件，則兩次訂貨間隔期t內的平均總費用
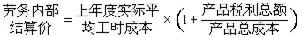。由微分學可知，若要求C(t) 最小，則當C(t)對t的導數等於零，即
求得最優訂貨間隔期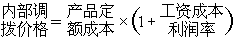
，經濟訂貨批量
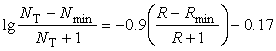，最小平均總費用
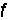。 隨機型庫存模型 這種庫存模型需求量是隨機的、離散的,當庫存量下降到某一數量I時即開始訂貨。它是在以下假設條件下建立的：①訂貨點（即提出訂貨時的庫存量）I已經確定;②單位物資價格為k,一批定貨的手續費為C3，當訂貨批量為Q時，所需訂貨費用為
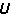；③單位物資平均庫存費用為C1，單位物資缺貨賠償費用為C2；④需求量為r，已知其機率為P(r),且
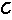；⑤庫存達到最高水平時的數量為S，即
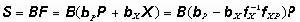。庫存總費用是s 的函式，可表達成：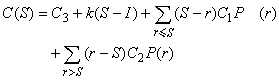 
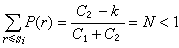
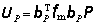。 當需求量和訂貨供應時間均為隨機的、離散的，則可套用蒙特卡羅法來確定最優訂貨批量和定貨點。
參考書目
李德等編:《運籌學》,清華大學出版社，北京，1982。
