基礎定義
在平面內,有公共端點的兩條射線組成的圖形叫做角,這兩條射線叫做角的邊,這個公共端點叫做角的頂點。
擴展定義
如果按照上述基礎定義來定義角的話,則角的度數只能限制在0°~360°內。因此在實際生活中,我們通常用另一種方式表示角:一條射線繞著它的端點 旋轉所形成的圖形叫做角,這條射線叫做角的始邊,旋轉到的位置所對應的邊叫做角的終邊,而這個公共端點叫做角的頂點。
角的概念被推廣後,便有了新的概念:我們通常把逆時針旋轉的角稱為正角,順時針旋轉的角稱為負角;如果沒有進行旋轉,也視為形成了一個角,這個角叫做零角。
要注意:正角和負角是表示具有相反意義的旋轉量,它的正負規定純屬習慣,就像與正數、負數的規定一樣。零角無正負,就像數零無正負一樣.
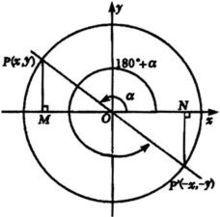
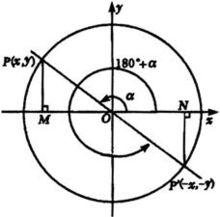 任意角
任意角象限角
為了研究方便,我們往往在平面直角坐標系中討論角。把角的頂點置於坐標原點,始邊與x軸的非負半軸重合,這樣一來,角的終邊落在第幾象限,就說這個角是象限角或說這個角屬於第幾象限;如果角的終邊在坐標軸上,就認為這個角不在任何象限
象限角的表示方法
第一象限k·360°+0°<α< k·360°+90° k∈z
第二象限k·360°+90°<α< k·360°+180° k∈z
第三象限k·360°+180°<α< k·360°+270° k∈z
第四象限k·360°+270°<α< k·360°+360° k∈z
軸線角
當角的頂點與坐標軸原點重合,角的始邊與x軸的非負半軸重合,那么角的終邊落在坐標軸上時,稱作軸線角(也稱象限界角),此時這個角不屬於任何象限。
表示方法
當角的始邊相同時,所有與角α終邊相同的角,連同角α在內可以用k·360°+α,k∈Z 或者用 k·2π+α,k∈Z來表示
(註:k·360°+α,k∈Z或 k·2π+α,k∈Z,不表示與角α終邊相同)
即任一與角α終邊相同的角,都可以表示成角α與整數個周角的和。
弧度制
我們知道,周角的360分之一為1度的角,用度作為單位來度量角的制度叫做角度制,1度等於60分,1分等於60秒。
但度、分、秒都是60進位制,在單位轉換上會造成很多麻煩,所以我們通常用另一種方式來度量角:將等於半徑長的圓弧所對的圓心角叫做1弧度的角,用符號rad表示,讀作弧度。用弧度作單位來度量角的制度叫做弧度制。以已知角a的頂點為圓心,以任意值R為半徑作圓弧,則a角所對的弧長L與R之比是一個定值﹝與R無關﹞,我們稱L=R時的正角為1弧度的角。以弧度為角的單位,稱此度量制為弧度制。
用弧度制表示角時,“弧度”和“rad”可以省略不寫;但角度制中的度(°)不可省略。
特點
前文提到,一條射線繞著它的端點 旋轉所形成的圖形叫做角,逆時針旋轉所形成的角稱為 正角;順時針轉動所形成的角稱為 負角;射線未作任何旋轉,仍留在原來位置,那么我們也把它看成一個角,叫做 零角。 無論採用角度制或弧度制,都能使角的集合與實數集合 R存在一一對應關係:每一個角都對應唯一的一個實數。 正角的弧度值是一個 正量(正實數),負角的弧度值是一個 負量(負實數),零角的弧度值是 零。
換算關係及扇形面積公式
360°=2π rad——→180°=π rad ——→1°= π / 180 rad≈0.01745 rad ——→1rad =180°/π ≈57.30°=57°18′,|a|=L/r ,S=1/2Lr ,1rad(即1弧度)=180÷π度 1rad×(180÷π)=角度
(參數說明:r為半徑,L為∠α所對的弧長,S為圓的面積)