簡介
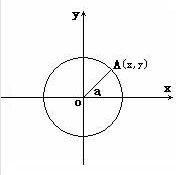任意角三角函式 任意角三角函式
在任意角三角形中，各邊角有以下的函式關係：
正弦定理在任意角三角形中，各個角的正弦與它所對的邊的比相等，並且等於外接圓的直徑。
餘弦定理在任意角三角形中，任意一邊的平方等於其餘兩邊的平方和減去這兩邊的乘積的兩倍與它們的夾角的餘弦的積。
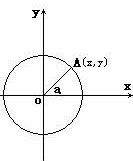
在直角坐標系中,⊙O的半徑為1,任意角α的三角函式定義如下:
正弦:∠α與單位圓的交點A的縱坐標與圓半徑的比值叫做正弦,表示為:sinα=Ay/OA=Ay；其中Ay叫做正弦線。
餘弦:∠α與單位圓的交點A的橫坐標與圓半徑的比值叫做餘弦,表示為:cosα=Ax/OA=Ax；其中Ax叫做餘弦線。
正切:∠α與單位圓的交點A的縱坐標與橫坐標的比值叫做正切,表示為:tanα=Ay/Ax；
餘切:∠α與單位圓的交點A的橫坐標與縱坐標的比值叫做餘切,表示為:cotα=Ax/Ay；；
正割:圓半徑和∠α與單位圓的交點A的橫坐標的比值叫做正割,表示為:secα=OA/Ax=1/Ax；
餘割:圓半徑和∠α與單位圓的交點A的縱坐標的比值叫做餘割,表示為:cscα=OA/Ay=1/Ay；
