概念
在統計學中,交叉表是矩陣格式的一種表格,顯示變數的(多變數)頻率分布。交叉表被廣泛用於調查研究,商業智慧型,工程和科學研究。它們提供了兩個變數之間的相互關係的基本畫面,可以幫助他們發現它們之間的相互作用。卡爾·皮爾遜(Karl Pearson)首先在“關於應變的理論及其關聯理論與正常相關性”中使用了交叉表。
多元統計學的一個關鍵問題是找到高維應變表中包含的變數的(直接)依賴結構。如果某些有條件的獨立性被揭示,那么甚至可以以更智慧型的方式來完成數據的存儲。為了做到這一點,可以使用信息理論概念,它只能從機率分布中獲得信息,這可以通過相對頻率從交叉表中容易地表示。
舉例
假設我們有兩個變數,性別(男性或女性)和手性(右或左手)。 進一步假設,從非常大的人群中隨機抽取100個人,作為對手性的性別差異研究的一部分。 可以創建一個應變表來顯示男性和右撇子,男性和左撇子,女性和右撇子以及女性和左撇子的個人數量。 這樣的應變表如下所示。
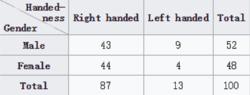 交叉表
交叉表男性,女性以及右撇子和左撇子個體的數量稱為邊際總數。總計(即應急表中所代表的個人總數)是右下角的數字。
這張表格讓我們一目了然地看到,右撇子男子的比例與右撇子女性的比例大致相同。兩種比例差異的意義可以通過各種統計檢驗來評估,包括Pearson的卡方檢驗,G檢驗,Fisher精確檢驗和巴納德檢驗,條件是表中的條目代表從人口我們想得出結論。如果不同列中的個體的比例在行之間變化很大(反之亦然),則我們說兩個變數之間存在偶然性。換句話說,這兩個變數不是獨立的。如果沒有偶然性,我們說這兩個變數是獨立的。
上面的例子是最簡單的交叉表,每個變數只有兩個級別的表:這被稱為2×2交叉表。原則上可以使用任何數量的行和列。也可能有兩個以上的變數,但較高階的偶然事件表難以在視覺上表示。序數變數之間或序數變數與分類變數之間的關係也可以用交叉表來表示,儘管這種做法很少見。
交叉表的標準內容
(1)多列(歷史上,它們被設計為占用列印頁面的所有空格)。 每個行指的是群體中的特定子組(例如男性),這些列有時稱為橫幅點(並且行有時稱為存根)。
(2)通常,任一列比較,其測試列之間的差異並使用字母顯示這些結果,其使用顏色或箭頭來標識以某種方式突出的表格中的單元格(如上例所示)。
(3)一個或多個:百分比,行百分比,列百分比,索引或平均值。
(4)未加權樣本大小(即計數)。
關聯度
兩個變數之間的關聯程度可以通過多個係數進行評估。 最簡單的,僅適用於2×2交叉表的情況,是由下式定義的phi係數:
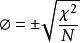 交叉表
交叉表其中χ2按照Pearson的卡方檢驗計算,N是觀察值的總和。 φ從0(對應於變數之間無關聯)變為1或-1(完全關聯或完全不關聯),前提是它基於2×2表中的頻率數據。 然後其符號等於表的主要對角線元素的乘積的符號減去非對角元素的乘積。 若且唯若每個邊際比例等於.50(兩個對角線單元為空)時,φ取最小值-1.00或最大值1.00。
備選方案包括四方相關係數(也僅適用於2×2表),交叉係數C、Cramér's V。
C的缺點是它不達到最大值1或最小值-1;在2×2表中可達到的最大值為0.707;在4×4表中可達到的最大值為0.870。在具有更多類別的應急表中,它可以達到接近1的值。 因此,它不套用於比較具有不同數目類別的表之間的關聯。此外,它不適用於不對稱表(行數和列數不相等的表)。
C和V係數的公式為:
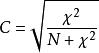 交叉表
交叉表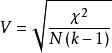 交叉表
交叉表k是行數或列數,以較小者為準。
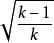 交叉表
交叉表可以通過將C除以在任意數量的行和列的表中完全關聯,使其最大值達到1。
四分相關係數假設每個二分法的基礎變數是常態分配的。四分相關係數提供了“等級測量已經減少到兩個類別時,相關性的便利度量。”四分位相關不應與通過分配計算的皮爾遜積矩相關係數相混淆 ,例如,值0和1表示每個變數的兩個級別(在數學上等於phi係數)。 涉及多於兩個等級變數的四方相關性的擴展是多相關係數。
λ係數是當標稱水平測量變數時交叉表的關聯強度的度量。 值範圍從0(無關聯)到1(理論最大可能關聯)。 不對稱lambda測量因變數預測的百分比改善。 對稱λ測量兩個方向進行預測時的百分比改善。
不確定係數是名義水平上變數的另一個測量。
交叉報表
交叉報表是報表當中常見的類型,屬於基本的報表,是行、列方向都有分組的報表。這裡牽涉到另外一個概念即分組報表。這是所有報表當中最普通,最常見的報表類型,也是所有報表工具都支持的一種報表格式。從一般概念上來講,分組報表就是只有縱向的分組。傳統的分組報表製作方式是把報表劃分為條帶狀,用戶根據一個數據綁定嚮導指定分組,匯總欄位,生成標準的分組報表。

