基本電路
定理闡釋
在只含一個電壓源（或電流源），不含受控源的線性電阻電路中，電壓源（或電流源）與電流表（電壓表）互換位置，電流表（電壓表）讀數不變。這種性質稱為互易定理。
互易定理即論述某些網路具有的互易性質的定理。互易性質表現為：將網路的輸入和特定輸出互換位置後,輸出不因這種換位而有所改變。具有互易性質的網路稱為互易網路。互易性不僅一些電網路有,某些聲學系統、力學系統等也有。互易定理是一個較有普遍意義的定理。
互易雙口
對於僅含線性時不變二端電阻和理想變壓器的雙口網路，稱為互易雙口。
對於互易雙口，存在以下關係，及所說的互易定理：
R=R
G=G
H=-H
TT-TT=1
性質
從圖中可以得出結論，圖(a)的電壓 u= R /S與圖(b)的電壓 u= R /S相同。也就是說，在互易網路中電流源與電壓表互換位置，電壓表讀數不變。
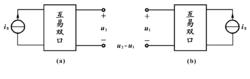交換電流源與電壓表圖(a)的電流 i2= G21 uS與圖的電流 i1= G12 uS相同。也就是說互易網路中電壓源與電流表互換位置，電流表讀數不變。
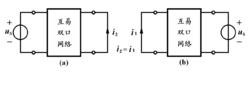交換電壓源與電流源套用條件
並非任何一個網路都具有互易性質。一般地說,由線性時不變的二端電阻元件、電感元件、電容元件、耦合電感器和理想變壓器連線而成的網路均有此性質。含有受控電源、非線性元件、時變元件、迴轉器的網路都不一定具有這種性質。
等效電路
由互易定理知道，互易雙口只有三個獨立參數，這就可以用右圖所示由三個電阻構成的Τ形或Ⅱ形網路等效。
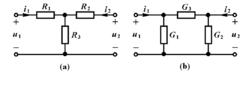互易定理等效電路圖(a)電路的網孔方程為：
U=R+(i+i)R
U=R+(R+R)i
與雙口流控表達上式對比，令其對應係數相等可以得到：
R=R+R
R=R+R
R=R=R
由此求得Τ形網路的等效條件為
R=R-R
R=R-R
R=R=R
用類似方法，可求得Ⅱ形網路的等效條件為：
G=G+G
G=G+G
G=-G=-G
電磁學
在電磁學上，互易定理為洛侖茲互易定理（Lorentz Reciprocity Theorem）,由卡森（J.R. Carson）導出而被稱為卡森形式的互易定理。
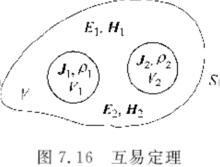互易定理互易定理可以利用麥克斯韋方程得到。設空間有兩組源J和J，分別產生的場為E、H和E、H，如圖所示
則
(1)兩個電流源J和J均在空間區域V外。
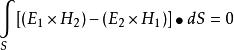互易定理上式稱為洛倫茲互易定理
(2)當V表示整個空間區時，S為無限大閉合面S∞。
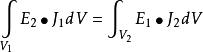互易定理上式稱為稱為卡森互易定理。
源與感測器
原理
源傳互易原理支持者的依據主要有二：一是所謂的熱力學證明，這已被證明為誤；另一依據則可以簡述如下：假定地表材料處處滿足Helmholz互易原理，從給定方向i射人M個光子，最終有N個光子從方向v到達感測器。那么從感測器以二的反方向射出M個光子，則必將有N個光子從i的反方向回到原位置。
如果論及的光源和感測器均為幾何點，這就是Helmholz互易原理本身。
證明與反論
假定兩者均遠離地面，因而人射光可視作平行光，而感測器最小感測單元也只接收地面對應像元反射向該感測單元的平行光，光源發出的平行光覆蓋這一像元周圍足夠大的鄰近區域，在地面和光源及感測器之間的大氣完全透明。我們進而假定光源發射的平行光是空間上均勻的，即在地物上方水平表面上有處處相同的人照。我們將稱這一緊貼地物最高點的水平面為參考表面，感測器在參考表面上形成的視場(即像元)為A。
如果A內以方向v向感測器的出射輻射是均勻的，也就是說，單位面積單位時間內射向感測器的光子數目處處相同，那末，我們總可以無限細分面積A，使得單位面積單位時間內每一個面積元平均一個光子射達感測器，共N個光子。
此時，我們假定以v的反方向，用同樣的平行光源，在足夠大的照明範圍內，以原人射光相同的密度(MA/)射人光子，那末，在A內入射的光子，將有N個循原路徑返回原人射位置。但迄今，我們仍未能證明源傳互易成立。由於地表結構的複雜性，從A射入的光子，可能在A外逸出，而A外射人的光子，可能在A內逸出。
光學互易定理
光柵互易定理
-1級Littrow入射條件在光柵的套用和理論上都占有非常重要的地位，該條件下有個著名的互易定理，定理闡述如下：
1）當一束TM平面波垂直入射到一理想導體三角槽形光柵的一個斜面上時，如果另一斜面的長度是半波長的整數倍，且這個光柵的槽頂角為90°，那么，這時光柵第m級衍射波的衍射效率是100%。這個定理也叫Marechal—Stroke定理。
2）當一束TM平面波以90°-α的入射角在-1級Littrow狀態下入射到閃耀角為α的階梯光柵上時，如果λ/d>2/3，那么-1級衍射波的衍射效率是100%。
由互易定理可以得到，在λ/d>2/3的波段範圍內，閃耀角互為餘角的兩個光柵在-1級Littrow狀態入射下具有相同的衍射效率。-1級Littrow入射條件下光柵的衍射效率最具有代表性，其他入射條件可以看成是該狀態下的近似，詳細研究此入射狀態下光柵的衍射效率對光柵的設計會起到事半功倍的作用。
亥姆霍茲定理
三度運算：標量場的梯度、矢量場的散度和鏇度，即場的性質的量度，矢量場的性質由其散度和鏇度確定：
亥姆霍茲定理可表示為，任一個矢量場由其散度、鏇度以及邊界條件所確定，都可以表示為一個標量函式的梯度與一個矢量函式的鏇度之和。
