運算符
位運算符:&(按位與)|(按位或)^(按位異或)~(按位取反)<<(按位左移)>>(有符號的按位右移)>>>(無符號的按位右移)
算術運算
二進制數的算術運算包括:加、減、乘、除四則運算,下面分別予以介紹。
(1)二進制數的加法
根據“逢二進一”規則,二進制數加法的法則為:
0+0=0
0+1=1+0=1
1+1=0 (進位為1)
1+1+1=1 (進位為1)
例如:1110和1011相加過程如下:
 二進制運算
二進制運算2)二進制數的減法
根據“借一有二”的規則,二進制數減法的法則為:
0-0=0
1-1=0
1-0=1
0-1=1 (借位為1)
例如:1101減去1011的過程如下 :
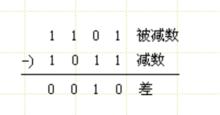 二進制運算
二進制運算(3)二進制數的乘法
二進制數乘法過程可仿照十進制數乘法進行。但由於二進制數只有0或1兩種可能的乘數位,導致二進制乘法更為簡單。二進制數乘法的法則為:
0×0=0
0×1=1×0=0
1×1=1
例如:1001和1010相乘的過程如下:
 二進制運算
二進制運算由低位到高位,用乘數的每一位去乘被乘數,若乘數的某一位為1,則該次部分積為被乘數;若乘數的某一位為0,則該次部分積為0。某次部分積的最低位必須和本位乘數對齊,所有部分積相加的結果則為相乘得到的乘積。
(4)二進制數的除法
二進制數除法與十進制數除法很類似。可先從被除數的最高位開始,將被除數(或中間餘數)與除數相比較,若被除數(或中間餘數)大於除數,則用被除數(或中間餘數)減去除數,商為1,並得相減之後的中間餘數,否則商為0。再將被除數的下一位移下補充到中間餘數的末位,重複以上過程,就可得到所要求的各位商數和最終的餘數。
例如:100110÷110的過程如下:
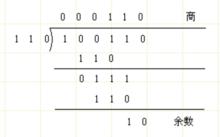 二進制運算
二進制運算所以,100110÷110=110餘10。
說明:乘除法分原碼乘法和補碼乘法。
邏輯運算
二進制數的邏輯運算包括邏輯加法(“或”運算)、邏輯乘法(“與”運算)、邏輯否定(“非”運算)和邏輯“異或”運算。
(1)邏輯“或”運算
又稱為邏輯加,可用符號“+”或“∨”來表示。邏輯“或”運算的規則如下:
0+0=0或0∨0=0
0+1=1或0∨1=1
1+0=1或1∨0=1
1+1=1或1∨1=1
可見,兩個相“或”的邏輯變數中,只要有一個為1,“或”運算的結果就為1。僅當兩個變數都為0時,或運算的結果才為0。計算時,要特別注意和算術運算的加法加以區別。
(2)邏輯“與”運算
又稱為邏輯乘,常用符號“×”或“· ”或“∧”表示。“與”運算遵循如下運算規則:
0×1=0或0·1=0或0∧1=0
1×0=0或1·0=0或1∧0=0
1×1=1或1·1=1或1∧1=1
可見,兩個相“與”的邏輯變數中,只要有一個為0,“與”運算的結果就為0。僅當兩個變數都為1時,“與”運算的結果才為1。
(3)邏輯“非”運算
又稱為邏輯否定,實際上就是將原邏輯變數的狀態求反,其運算規則如下:
可見,在變數的上方加一橫線表示“非”。邏輯變數為0時,“非”運算的結果為1。邏輯變數為1時,“非”運算的結果為0。
(4)邏輯“異或”運算
“異或”運算,常用符號“”或“”來表示,其運算規則為:
00=0 或 00=0
01=1 或 01=1
10=1 或 10=1
11=0 或 11=0
可見:兩個相“異或”的邏輯運算變數取值相同時,“異或”的結果為0。取值相異時,“異或”的結果為1
以上僅就邏輯變數只有一位的情況得到了邏輯“與”、“或”、“非”、“異或”運算的運算規則。當邏輯變數為多位時,可在兩個邏輯變數對應位之間按上述規則進行運算。特別注意,所有的邏輯運算都是按位進行的,位與位之間沒有任何聯繫,即不存在算術運算過程中的進位或借位關係。下面舉例說明 。
【例1.1】 如兩變數的取值 X=00FFH, Y=5555H
求 Z1= X∧ Y; Z2= X∨ Y; Z3=; Z4= X Y的值。
解: X=0000000011111111
Y=0101010101010101
則: Z1=0000000001010101=0055H
Z2=0101010111111111=55FFH
Z3=1111111100000000=FF00H
Z4=0101010110101010=55AAH

