久期方程

久期方程是對任意線性齊次方程組而言的。任意線性齊次方程組有根的條件是其係數行列式為零。這說明幾個方程不是線性無關的，即至少有一組線性相關的解組。一般用久期方程判斷方程組有無根的性質來確定某方程組的係數。

概念

在原子軌道線性組合為分子軌道中，久期方程是指關於組合係數的線性齊次方程組。該方程組有不全為零的解的條件是由係數所構成的行列式等於零，此行列式稱為久期行列式。

久期方程是對任意線性齊次方程組而言的。任意線性齊次方程組有根的條件是其係數行列式為零。這說明幾個方程不是線性無關的，即至少有一組線性相關的解組。一般用久期方程判斷方程組有無根的性質來確定某方程組的係數。

基本原理

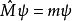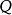久期方程

久期方程

本徵值方程 在一定的表象 中可以寫成矩陣形式，如圖1所示：

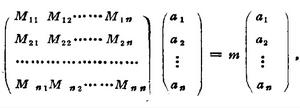圖1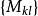

久期方程

久期方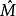程

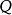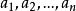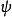久期方程

久期方程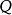

久期方程

久期方程

其中矩陣 是算符 在 表象中的矩陣表示，由 構成的列矩陣是波函式 在 表象中的表示。上述方程可變形為如圖2所示：

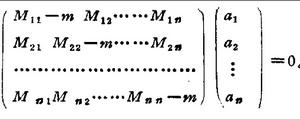圖2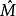

久期方程

久期方程

由此可解得算符 的一系列本徵值 和相應的本徵函式。非零本徵函式存在的條件是上述代數方程的係數行列式為零，即如圖3所示：

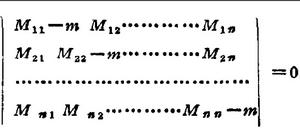圖3

此方程稱為久期方程。