係數使用
風險敏感係數是風險管理至關重要的工具。 每個風險敏感係數度量投資組合在指定的標的微小變化時的敏感性，因此風險的組成部分都可以被單獨度量，並且資產組合能夠根據所需的暴露風險進行再平衡。
風險敏感係數在布萊克-肖爾斯期權定價模型中相對比較容易計算，並且可以由金融模型來推導得到性質，它對於衍生品交易員來說非常重要，尤其是對於有對沖價值的風險敏感係數Delta, Theta 和Vega都被很好的用來用來度量標的價格，時間和波動率的變化。 儘管Rho在布萊克－肖爾斯模型中是主要的輸入變數，但是無風險利率的相應變化對於期權價格的總體影響一般是微不足道的。所以包含無風險利率的高階導數並不常用。
最常見的風險敏感係數有價值函式的一階導數 Delta, Vega, Theta 和 Rho 以及二階導數Gamma。此表中的其他敏感性非常常見，所以他們也有常見的名字，但是詞表只包含部分內容，並不詳盡。
風險敏感係數
| 即期價格 | 波動率 | 到期時間 | |
| 現值 | Delta | Vega | Theta |
| Delta | Gamma | Vanna | Charm |
| Vega | Vanna | Vomma | Veta |
| Gamma | Speed | Zomma | Color |
| Vomma | Ultima | Totto | |
| 的定義是期權的價格和風險（第一列）對於標的資產（第一行）的敏感度 。其中現值對應的行是一階風險敏感係數，Delta和Vega對應的行是二階風險敏感係數，Gamma和Vomma對應的行是三階風險敏感係數。 | |||
一階希臘字母
Delta
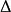風險敏感係數Delta ， ，衡量的是理論期權價值相對於標的資產價格變化的變化率。 Delta是期權價值V對標的價格S的一階導數。
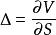風險敏感係數實際使用
對於標準化期權，Delta在買入看漲期權（賣出看跌）中會是一個介於0到1之間的數字；在買入看跌期權（賣出看漲）時這個數字是0或者－1。 看漲期權取決於標的價格，其表現如同擁有一股標的股票（如果是價內期權）或者什麼也沒有（如果是價外期權），或者介於兩者之間,對於看跌期權反之亦然。同樣的執行價格的看漲期權和看跌期權的Delta的不同之處在於非常接近但是一般不等於1，而是等於折現率的倒數。根據買賣權平價關係同時買入看漲期權和賣出看跌期權等於買入一份期貨F，此期貨與現貨S呈線性關係，該線性方程中的係數是折現率的倒數，所以導數dF/dS就正好是這個係數。
這些數字一般用期權契約(S)占總數的百分比的形式呈現。這樣會比較方便表達，因為期權會（立即）呈現出由 Delta所代表的股數。例如，假設一個包含100股美式看漲期權的XYZ的資產組合其中每一個的Delta都是0.25（=25%），那么這個資產組合隨著價格的微小變動就會盈利或者虧損類似25股XYZ的情況。Delta表達時正負號和百分比通常會被省略－因為正負號是隱含在期權種類中的（看跌表示負號，看漲表示正號），然後百分比也很好理解。最常見的表述是25-Delta的看跌期權，50-Delta的看跌期權，50-Delta的看漲期權和25-Delta 的看漲期權。50-Delta看跌期權 和50-Delta看漲期權並不完全一樣，這是因為有了折現係數的存在，即期和遠期是不一樣的，但是他們通常被視為等價。
Delta一般對於買入看漲期權總是為正，對於買入看跌期權總是為負（除非他們為零）。一個複雜的資產組合對於同樣標的資產的頭寸的總的Delta 可以通過分別取每種頭寸的Delta總和來得到。這個資產組合的Delta是一個線型函式。
因為標的資產的Delta總是1，所以交易員可以通過買賣總Delta所表示數量的數額來無風險對沖他的所有標的頭寸。例如，如果一種資產組合XYZ (他們的表達方式為標的資產的一定份額) 的Delta 是+2.75， 那么交易員就能夠通過賣空2.75股標的資產進行無風險對沖。然後這種資產組合就能一直保持其總價值，不論XYZ的價格會往哪個方向變動（儘管只是標的資產的小幅度的變化，很短時間內變化，在其他例如波動和無風險投資回報率的其他市場情況下除外）。
作為機率替代
Delta （絕對值）接近但是不完全等於期權的價值狀態的百分比，例如會使價內期權失效的隱含機率（如果市場走勢在風險中性測量遵循布朗運動）。由此，一些期權交易員用Delta的絕對值作為貨幣狀態百分比的近似值。舉個例子，如果一個價外看漲期權的delta是0.15，那么交易員就會估計期權大概有15%的可能性價內失效。同樣的，如果一個看跌期權的Delta值為－0.25，交易員就可能會預計期權有25%的可能性價內失效。平值看跌看漲期權的Delta值大概分別為0.5和－0.5，對於平值期權會有高一點的Delta的微小偏差。也就是說，兩者都有大約50%的可能性價內失效。確切的對於在某個特定價格K結束期權可能性的計算是它的對偶期權，也就是期權價格對於執行價格的一階導數。
看漲和看跌Delta的關係
給定同一個標的物的歐式看漲和看跌期權，執行價格和到期時間，沒有股息收益，那么每種期權Delta絕對值的總和為1，更確切的說，看漲期權的Delta（正數）減去看跌期權的Delta（為負數）等於1。這是因為買賣權平價理論：買入看漲期權加上賣出看跌（看漲減去看跌）跟一個Delta值等於1的遠期契約是一樣的。
如果某種期權的Delta值是已知的，就可以計算同樣執行價格，標的資產和到期時間但是相反方向權利的期權的Delta值，也就是從已知的看漲Delta減去1或者把已知的看跌Delta加上1。
D(看漲)－D(看跌)=1。 因此，D（看漲）=D（看跌）+1； D（看跌）=D（看漲）－1。
例如，如果一個看漲期權的Delta值是0.42，那么我們就可以計算相對應的同樣執行價格的看跌期權為0.42-1=－0.58。如果已知看跌期權Delta要計算看漲Delta，類似的計算－0.58+1=0.42 。
Vega
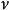風險敏感係數Vega， ，測量的是期權波動率的敏感度，它是期權價值相對於標的資產波動率的導數。
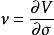風險敏感係數 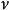風險敏感係數Vega 不是任何希臘字母的名稱，然而它使用的的字形是希臘字母nu ( )。據推測，Vega這個名稱的使用是因為希臘字母nu 看起來像拉丁字母Vee，然後類比Beta, Eta和Theta在美式英語中的發音，Vega就從Vee衍生而來。另一個可能是它以Joseph De La Vega命名。此人因一本研究股票市場和涉及到期權和遠期交易的複雜的交易行為的著作而聞名於世，書名為《Confusion of confusions》。
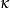風險敏感係數符號kappa， ，有時候（在學術中）被用來替代Vega。
Vega 通常被表述為期權價值每標的份額隨著波動性上升或下降1%所獲得的收益或者造成的損失的金額。
Vega 對於期權交易員來說是很重要的希臘字母，尤其是在動盪的市場上，因為一些期權策略的價值在波動性中對於變化非常敏感。例如期權套期圖利，就非常依賴於對於波動性的變化。
Theta
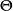風險敏感係數Theta， ，測量的是衍生品價值對於時間推移的敏感性，也就是“時間衰減”。
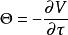風險敏感係數Theta的這個公式的數學結果是按年計算的。按照慣例，通常要把這個結果除以一年的天數，來得到一天中每股標的資產損失的金額。Theta對於買入看漲或者看跌期權來說一般是負數；對於賣出看跌或者看漲期權來說一般是正數。有一個例外就是深度價內歐式看跌期權。期權資產組合的Theta 的可以通過加總每個單獨的頭寸的Theta值來計算。
一種期權的價值可以分為兩個部分：內含價值和時間價值。內含價值是你立即執行期權契約將會獲得的收益，所以一份執行價格為$50，價格為$60的股票期權契約的內含價值就是$10，但是相對應的看跌期權的內含價值就是0。時間價值就是擁有一份在決定執行契約前等待更長時間的價值。即使是一份看跌的價外期權也是有價值的，因為還是有股票價格在到期日前下跌到執行價格之下仍舊具有T可能性。然而，隨著時間越來越趨近到期日，這種情況發生的可能性就會越來越小，所以期權的時間價值是隨著時間遞減的。因此如果你買入一種期權就意味著你就看空Theta，即其他因素不變的情況下你持有的資產組合會隨著時間失去價值。
Rho
風險敏感係數Rho， ， 度量的是對於利率的敏感性，它是期權價值相對於無風險利率的導數。
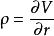風險敏感係數除了在極端情況下，期權的價值對於無風險利率的變化比對於其他參數變化的敏感度更低。因此，Rho在一階希臘字母中是最不常用的。
Rho 一般被表述為每股標的資產的期權隨著無風險利率上升或者下降1.0%每年（100個基本點）所收益或損失的金錢的數額。
Lambda
風險敏感係數
風險敏感係數Lambda， ， omega， ，或者稱為彈性，是期權價值對於標的資產價格每百分比變化的百分比變化。它是一種槓桿方式，有時候被稱作槓桿比率。
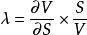風險敏感係數二階希臘字母
Gamma
風險敏感係數Gamma， ，測量的是Delta對於標的資產價格變化的變化率。
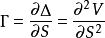風險敏感係數Gamma 是價值方程相對於標的價格的二階導數。所有的買入期權都有正的Gamma，所有賣出期權都有負的Gamma。買入期權與Gamma正相關是因為隨著價格的上升，Gamma也會上升，從而使Delta從0趨向於1（對於買入看漲期權）或使之從0趨向於－1（對於買入看跌期權）。對於賣出期權反之亦然。
風險敏感係數Gamma 最近似於平價期權，隨後不論是變為價內期權還是價外期權，這種近似關係都會慢慢消失。Gamma很重要是因為它更正了價值的凸性。
當一個交易員尋求建立一種對資產組合有效的無風險對沖，這個交易員就可能會使這個資產組合的Gamma中性，因為這樣可以保證對沖在更廣泛為的標的價格變動時有效。然而，在中和一種資產的Gamma時，資產的Alpha（超過無風險利率的回報）也被減少了。
Vanna
Vanna，也被稱為DvegaDspot 和DdeltaDvol，是期權價值的二階導數,第一次對標的價格，第二次對波動性求導。它在數學上等價於DdeltaDvol, 也就是期權Delta相對於波動性變化的敏感度，或者Vega對標的資產價格的偏導。Vanna是一個很有用的用於監測保持Delta或者Vega對沖資產組合的敏感度測量，因為Vanna能夠幫助交易員來預測無風險對沖隨著波動率變化的有效性而變化或者Vega對沖對於標的即期價格變化的有效性。
如果標的價值方程具有連續的二階偏導，那么其計算公式如下。
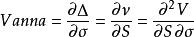風險敏感係數Vomma
Vomma，Volga，Vega convexity，Vega Gamma 或者d Tao/d Vol 測量的都是對於波動性的二階導數。
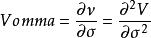風險敏感係數Vomma 是期權價值對於波動性的二階導數。如果Vomma為正數，隨著隱含波動性的增加，Vega頭寸會被看漲；如果隱含波動性降低，會看空Vega,這在某種程度上類似看漲Gamma。一份起初Vega中性，看漲Vomma的頭寸可以根據不同執行價格的期權份額來構造。對於理論上沒有價值的期權，Vomma是正數，起初會隨著價格偏離的程度而增加（但是隨著Vega的下降也會下降）。（特別需要指出的是，一般d1 和d2是同一個符號，而Vomma為正數，當d2<0 或者d1>0時也同樣成立。）
Charm
Charm 或者Delta衰減，衡量的是Delta相對於相對於時間流逝的即使變化率，也被稱作DdeltaDtime。Charm 在衡量或者監測超過周末的無風險對沖頭寸的頭寸時很有用。Charm是期權價值的二階導數，第一次是對價格，第二次是對時間。它同時也是Theta對於標的價格導數。
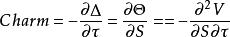風險敏感係數Charm的公式表達的數學結果為d Delta/d time。通常也用它來除以每年的天數來得到每天的Delta的衰減率。特別是當距離期權到期日時間比較長時，這種處理就非常確切。如果距離到期日很近，Charm本身就會變得比較快，會使Delta衰減的每天估計不準確。
Veta
Veta， 或者DvegaDtime，測量的是Vega相對於時間的變化率。Veta是價值方程的二階導數，第一次是對波動性，第二次是對時間。
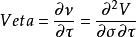風險敏感係數通常的做法是通過用得到的數學結果除以天數再除以100，從而減小Vega每天每一百分比的變化值。
Vera
Vera, 或者DvegaDtime, 測量的是Rho相對於波動性的變化率。Vera是價值方程的二階導數，第一次是對波動性，第二次是對利率。Vera可以被用來波動性變化對Rho對沖的影響。
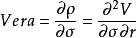風險敏感係數三階希臘字母
Color
Color， Gamma衰減或者DgammaDtime，是測量對Gamma對時間的變化率。Color是加之方程的三階導數，兩次對標的資產，一次對時間。Color是判斷是否維持Gamma對沖資產時很有用的敏感度係數，因為它可以幫助交易員預測對沖對時間的有效性。
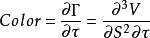風險敏感係數Color公式的數學表達式是d Gamma/d time。它通常會除以一年的天數來得到每天的Gamma改變數。當離到期日比較遠時這個字母的作用會比較準確，但是當期權接近到期日時，Color本身就變得非常快，所以對於Gamma的每天估計會不太準確。
Speed
Speed測量的是Gamma相對於標的價格的變化率。有時候也被稱為Gamma的Gamma或者DgammaDspot。Speed是價值方程相對於標的物即期價格的三階導數。在監管無風險對沖或者Gamma對沖一個資產組合時，Speed是很有用的。
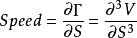風險敏感係數Ultima
Ultima測量的是期權的Vomma相對於波動性變化的敏感度。 Ultima也被稱作DvommaDvol。Ultima是期權價值對波動性的三階導數。
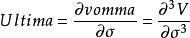風險敏感係數Zomma
Zomma測量的是Gamma相對於波動率變化的變化率。Zomma也被稱作DgammaDvol。Zomma是期權價值的三階導數，兩次對標的資產價格，一次對波動性。Zomma是確保Gamma對沖資產時很好的敏感度指標，這是因為Zomma可以幫助交易員預測對沖有效性隨著波動性變化的變化。
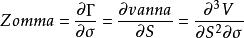風險敏感係數多資產期權
如果衍生品的價值依賴於兩種及以上標的資產，那么它的希臘字母就被擴展為包含標的資產的交叉效應。
關聯Delta 測量的是衍生品價值對於標的資產之間相關性變化的敏感度。
交叉Gamma 測量的是一種標的資產對另一種標的資產水平上的變化的Delta的變化率。
交叉Vanna 測量的是Vega的一種標的資產因為另一種水平上的標的資產的變化而產生的變化率。同樣的，它測量的是第二種標的資產由於第一種標的資產波動率變化而產生的Delta 的變化率。
交叉Volga 測量的是一種標的資產對於另一種標的資產波動性變化的變化率。
相關度量
一些相關的金融衍生品風險度量的方法如下。
久期和凸性
在交易固定收益證券（債券）時，各項測量債券久期的方式是類似於期權的Delta的。跟Delta最為接近的是DV01（dollar duration，美元久期 ），也就是每一個基本點的上升為（即0.01%每年）所帶來的收益率（收益是標的資產變數）價格（貨幣單位）的下跌。
類似於Lambda的是修正久期，也就是債券價格市場價格變化的百分比對於收益率一單位變化（及它等於DV01除以市場價格）。不同於Lambda（一個彈性，即輸出的對於百分比的輸入的百分比的變化），修正久期是半彈性－輸出對於一單位輸入變化的百分比變化。
債券凸性是一種測量久期對於利率變化的敏感度的工具，也是債券價格對於利率的二階導數（久期是一階導數）。一般情況下，凸性越大，債券價格對於利率變化的敏感度越大。債券凸性是最基本和套用最廣泛的金融凸性的一種。
Beta
風險敏感係數股票或者資產組合的Beta ()是一個描述一種資產的波動性和與之相對比的基準的波動性的關係的數字。這個基準通常是整個金融市場，一般用代表指數，例如標準普爾500來估計得到。
如果一種資產的回報率的變化不依賴於市場回報率的話，這種資產的Beta就是0。正的Beta意味著這種資產的回報率一般遵循市場回報率，在這個意義上他們都會比各自在一起的平均值更高，或者低於各自在一起的平均值。一個負的Beta意味著資產的回報率一般與市場回報率向反方向移動：當另外一方低於平均值時，它會高於兩者的平均值。
Fugit
Fugit 是執行一份美式期權或者百慕達期權的預期時間。對於對沖目的之用，計算Fugit是非常有用的－例如，可以用開始於Fugit乘以Delta的互換來代表美式互換期權，然後用這些來計算敏感性。
