基本概念
 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子設 是n階一矩陣,k是小於等於n的某個正整數,如果 的所有k階子式的最大公因子(它是首一多項式)不等於零,則稱這個多項式為 的k階 行列式因子,記為 。如果 的所有k階子式都等於零,則規定 的k階行列式因子為零。
定義
 不變因子
不變因子 不變因子
不變因子 不變因子
不變因子設 是一矩陣 A( )的非零行列式因子,則
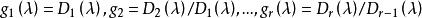 不變因子
不變因子 不變因子
不變因子稱為A( )的 不變因子。
相關定理
定理1
相抵的λ一矩陣有相同的行列式因子,從而有相同的不變因子。
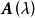 不變因子
不變因子證明 我們只需證明行列式因子在任意一種初等變換下不變就可以了,對第一種初等變換,交換λ一矩陣的任兩行,顯然 A(λ )的i階子式最多改變一個符號,因此行列式因子不改變。
對第二種初等變換, A(λ )的i階子式與變換後矩陣的i階子式最多差一個非零常數,因此行列式因子也不改變。
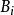 不變因子
不變因子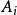 不變因子
不變因子對第三種初等變換,記變換後的矩陣為 B(λ ),則 B( λ)與 A(λ )的i階子式可能出現以下3種情形:子式完全相同; B(λ )子式中的某一行(列)等於 A(λ )中相應子式的同一行(列)加上該子式中某一行(列)與某個多項式之積; B(λ )子式的某一行(列)等於 A( λ)中相應子式的同一行(列)加上不在該子式中的某一行(列)與某個多項式之積,在前面兩種情形,行列式的值不改變,因此不影響行列式因子,現在來討論第三種情形,設 為 B(λ )的t階子式,相應的 A( λ)的i階子式記為 ,則由行列式性質得
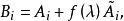 不變因子
不變因子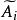 不變因子
不變因子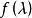 不變因子
不變因子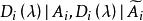 不變因子
不變因子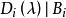 不變因子
不變因子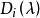 不變因子
不變因子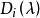 不變因子
不變因子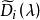 不變因子
不變因子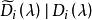 不變因子
不變因子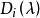 不變因子
不變因子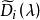 不變因子
不變因子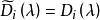 不變因子
不變因子其中 由 A( λ)中的i行與i列組成,因此它與 A( λ)的某個i階子式最多差一個符號, 是乘以某一行(列)的那個多項式,於是 A( λ)的行列式因子 ,故 ,這說明, 可整除 B(λ)的所有i階子式,因此 可整除 B(λ )的i階行列式因子 ,但 B( λ)也可用第三種初等變換變成 A( λ),於是 ,由於 及 都是首一多項式,因此必有 。
推論1
設n階 λ一矩陣 A( λ)的法式為
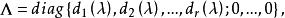 不變因子
不變因子 不變因子
不變因子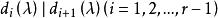 不變因子
不變因子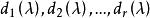 不變因子
不變因子其中 是非零首一多項式且 ,則 A(λ )的不變因子為 .特別,法式和不變因子之間相互唯一確定。
 不變因子
不變因子 不變因子
不變因子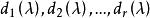 不變因子
不變因子證明 由定理1, A(λ )與 有相同的不變因子, 的不變因子為 ,從而它們也是 A(λ )的不變因子。
推論2
設 A(λ ), B( λ)為n階 λ一矩陣,則 A(λ )與 B( λ)相抵若且唯若它們有相同的法式。
證明 若 A( λ)與 B( λ)有相同的法式,顯然它們相抵,若 A( λ)與 B( λ)相抵,由定理1知 A( λ)與 B( λ)有相同的不變因子,從而有相同的法式。
推論3
n階 λ一矩陣 A(λ )的法式與初等變換的選取無關。
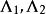 不變因子
不變因子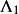 不變因子
不變因子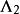 不變因子
不變因子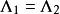 不變因子
不變因子證明 設 是 A( λ)通過不同的初等變換得到的兩個法式,則 與相抵,由推論2可得。
定理2
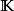 不變因子
不變因子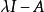 不變因子
不變因子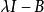 不變因子
不變因子數域 上n階矩陣 A與 B相似的充分必要條件是它們的特徵矩陣 和 具有相同的行列式因子或不變因子。
證明 顯然不變因子與行列式因子之間相互唯一確定,再由定理2,推論1及推論2即得結論。
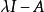 不變因子
不變因子之後特徵矩陣 的行列式因子及不變因子均簡稱為 A的行列式因子與不變因子。
推論4
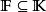 不變因子
不變因子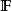 不變因子
不變因子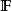 不變因子
不變因子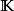 不變因子
不變因子設 是兩個數域, A, B是 上的兩個矩陣,則 A與 B在 上相似的充分必要條件是它們在 上相似。
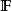 不變因子
不變因子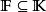 不變因子
不變因子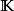 不變因子
不變因子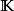 不變因子
不變因子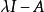 不變因子
不變因子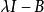 不變因子
不變因子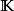 不變因子
不變因子 不變因子
不變因子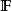 不變因子
不變因子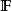 不變因子
不變因子 不變因子
不變因子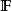 不變因子
不變因子 不變因子
不變因子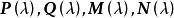 不變因子
不變因子證明 若 A與 B在 上相似,由於 ,它們當然在 上也相似,反之,若 A, B在 上相似,則 與 在 上有相同的不變因子,也就是說它們有相同的法式,但在求法式的過程中只涉及多項式的加、減、乘及數的加、減、乘、除運算,而數域在加、減、乘、除運算下封閉,數域上的多項式在加、減、乘及數乘下也封閉,因此由推論3,法式中的不變因子多項式 仍是 上的多項式,與初等變換相對應的初等矩陣也是 上的 一矩陣,這就是說存在 上的可逆 一矩陣 ,使
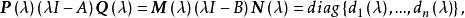 不變因子
不變因子從而
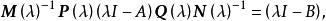 不變因子
不變因子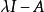 不變因子
不變因子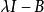 不變因子
不變因子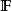 不變因子
不變因子 不變因子
不變因子即 與 在 上相抵,由定理2可得 A與B在 上相似。

