定義和例子
 初等因子
初等因子 初等因子
初等因子把矩陣 的每個次數大於零的不變因子分解成互不相同的首項為1的一次因式方冪的乘積,所有這些一次因子方冪(相同的必須按出現的次數計算)稱為矩陣 的 初等因子 。
例1 設12級矩陣的不變因子是
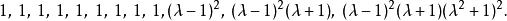 初等因子
初等因子按定義,它的初等因子有7個,即
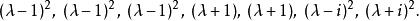 初等因子
初等因子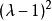 初等因子
初等因子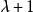 初等因子
初等因子其中 出現三次, 出現兩次 。
不變因子和初等因子的關係
 初等因子
初等因子 初等因子
初等因子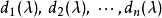 初等因子
初等因子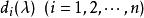 初等因子
初等因子首先,假設 級矩陣 的不變因子 為已知。將 分解成互不相同的一次因式方冪的乘積:
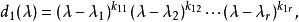 初等因子
初等因子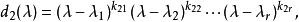 初等因子
初等因子 初等因子
初等因子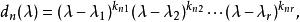 初等因子
初等因子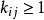 初等因子
初等因子則其中對應於 的那些方冪
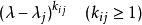 初等因子
初等因子 初等因子
初等因子就是 的全部初等因子。我們注意不變因子有一個除盡一個的性質,即
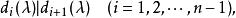 初等因子
初等因子從而
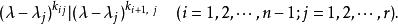 初等因子
初等因子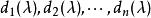 初等因子
初等因子因此,在 的分解式中,屬於同一個一次因式的方冪的指數有遞升的性質,即
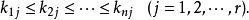 初等因子
初等因子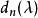 初等因子
初等因子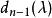 初等因子
初等因子這說明,同一個一次因式的方冪作成的初等因子中,方次最高的必定出現 在 的分解中,方次次高的必定出現 在 的分解中。如此順推下去,可知屬於同一個一次因式的方冪的初等因子在不變因子的分解式中出現的位置是惟一確定的。
 初等因子
初等因子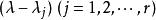 初等因子
初等因子 初等因子
初等因子 初等因子
初等因子 初等因子
初等因子上面的分析給了我們一個如何從初等因子和矩陣的級數惟一地作出不變因子的方法。設一個 級矩陣的全部初等因子為已知,在全部初等因子中將同一個一次因式 的方冪的那些初等因子按降冪排列,而且當這些初等因子的個數不足 時,就在後面補上適當個數的 ,使得湊成 個。設所得排列為
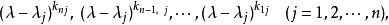 初等因子
初等因子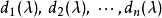 初等因子
初等因子 初等因子
初等因子則 就是 的不變因子。
這也說明了這樣一個事實:如果兩個同級的數字矩陣有相同的初等因子,則它們就有相同的不變因子,因而它們相似。反之,如果兩個矩陣相似,則它們有相同的不變因子,因而它們有相同的初等因子。
定理1
兩個同級複數矩陣相似的充要條件是它們有相同的初等因子 。
初等因子和不變因子都是矩陣的相似不變數,但是初等因子的求法與不變因子的求法相比,反而方便一些。
在介紹直接求初等因子的方法之前,先來說明關於多項式的最大公因子的一個性質:
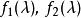 初等因子
初等因子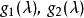 初等因子
初等因子如果多項式 都與 互素,則
 初等因子
初等因子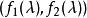 初等因子
初等因子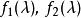 初等因子
初等因子其中 表示 的最大公因子。
定理2
設
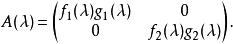 初等因子
初等因子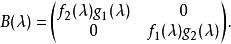 初等因子
初等因子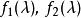 初等因子
初等因子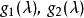 初等因子
初等因子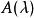 初等因子
初等因子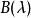 初等因子
初等因子如果多項式 都與 互素,則 和 等價。
下面的定理給了我們一個求初等因子的方法,它不必事先知道不變因子。
定理3
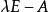 初等因子
初等因子 初等因子
初等因子首先用初等變換化特徵矩陣 為對角形式,然後將主對角上的元素分解成互不相同的一次因式方冪的乘積,則所有這些一次因式的方冪(相同的按出現的次數計算)就是 的全部初等因子。
