方法簡介
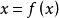 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法不動點法(fixed point method)是解方程的一種一般方法,對研究方程解的存在性、唯一性和具體計算有重要的理論與實用價值。數學中的各種方程,諸如代數方程、微分方程和積分方程等等,均可改寫成的形式,其中是某個適當的空間中的點,是從到的一個映射,把點變成點。於是,方程的解就相當於映射在空間中的不動點。這一方法把解方程轉化為求某個映射的不動點,故而得此名。其優點在於可以把幾何、拓撲和泛函分析中較深刻的工具套用於方程論。
舉例說明
例如,為求常微分方程初值問題
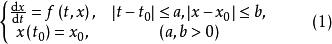 不動點法
不動點法的解,可以先把它化為一個等價的伏爾泰拉(Vito Volterra)型積分方程
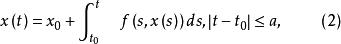 不動點法
不動點法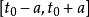 不動點法
不動點法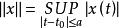 不動點法
不動點法如果把區間上的所有連續函式x的全體在範數下的空間記為X,從X到X的運算元 T定義為
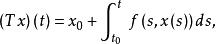 不動點法
不動點法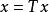 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法則積分方程(2)相當於運算元方程。於是原初值問題(1)就轉化成求在中的不動點的問題了。而後者可以利用拓撲或泛函分析中的不動點定理來解決。至於各種微分方程的邊值問題可以套用格林(Green)函式化成弗雷德霍姆(Fredholm)積分運算元的不動點問題。
注意點
在套用不動點方法研究方程的解時有兩個重要的準備工作。一是把方程化成合適的運算元方程;二是選擇合適的空間並在其中找方程的解。(可參考上述例題理解)。
不動點定理
常用的不動點定理有巴拿赫(Banach)不動點定理,布勞威爾(Brouwer)不動點定理和紹德爾(Schauder)不動點定理等等。
Banach不動點定理
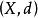 不動點法
不動點法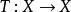 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法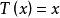 不動點法
不動點法設是完備的距離空間,是壓縮映射,則有惟一的不動點,即存在惟一的,使。
Brouwer不動點定理
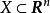 不動點法
不動點法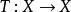 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法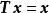 不動點法
不動點法設是緊凸集,映射是連續的,則有不動點,即存在,使。
後來,Schander把Brouwer不動點定理推廣到空間為無窮維的情形,Kakutani又把Brouwer不動點定理推廣到集值映射的情形。
Schauder不動點定理
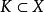 不動點法
不動點法 不動點法
不動點法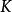 不動點法
不動點法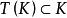 不動點法
不動點法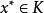 不動點法
不動點法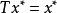 不動點法
不動點法設X是實的Banach空間,是有界閉凸集,全連續運算元映到自身,即,則存在,使。
Kakutani不動點定理
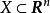 不動點法
不動點法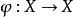 不動點法
不動點法 不動點法
不動點法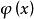 不動點法
不動點法 不動點法
不動點法 不動點法
不動點法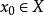 不動點法
不動點法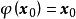 不動點法
不動點法設是凸緊集,集值映射是上半連續的,且對任,是中的非空凸集,則有不動點,即存在,使。

