重積分的定義
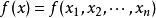 三重積分換元法
三重積分換元法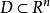 三重積分換元法
三重積分換元法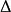 三重積分換元法
三重積分換元法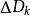 三重積分換元法
三重積分換元法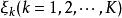 三重積分換元法
三重積分換元法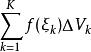 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法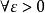 三重積分換元法
三重積分換元法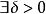 三重積分換元法
三重積分換元法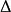 三重積分換元法
三重積分換元法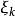 三重積分換元法
三重積分換元法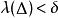 三重積分換元法
三重積分換元法設函式 在可求體積的有界閉區域 上有定義, 為D的一個分割。在每個 上任取一點 ,作黎曼和 。如果存在常數 ,使得對於 , ,對D的任何分割 以及任意選取的 ,當 時,有
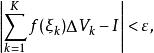 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法則稱f在D上 可積,並且稱 為f在D上的n 重積分,記為
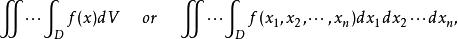 三重積分換元法
三重積分換元法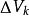 三重積分換元法
三重積分換元法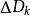 三重積分換元法
三重積分換元法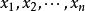 三重積分換元法
三重積分換元法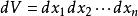 三重積分換元法
三重積分換元法其中,f稱為 被積函式,D稱為 積分區域,為的體積, 稱為 積分變數, 稱為 體積元素 。
在上述定義在中,特別地,當n=2時,我們常常記被積函式為f(x,y) ,此時,f(x,y)在D上的二重積分記為
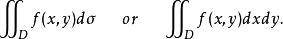 三重積分換元法
三重積分換元法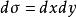 三重積分換元法
三重積分換元法這時也稱 為面積元素。當n=3時,記被積函式為f(x,y,z),則f(x,y,z)在D上的三重積分記為
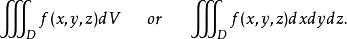 三重積分換元法
三重積分換元法三重積分換元法
類似二重積分,對於三重積分也有下面的換元法。
定理1
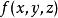 三重積分換元法
三重積分換元法設三元函式 在有界閉體V上連續,又設函式組
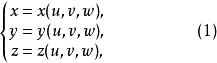 三重積分換元法
三重積分換元法在uvw空間中的有界閉體V'上有定義。若下列條件滿足:
(1)函式組(1)將uvw空間中的體V'一對一地變換到xyz空間中的體V;
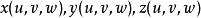 三重積分換元法
三重積分換元法(2)函式 所有一階偏導數在V'上連續;
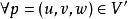 三重積分換元法
三重積分換元法(3) ,有
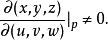 三重積分換元法
三重積分換元法則
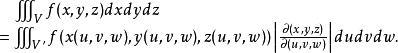 三重積分換元法
三重積分換元法注 定理的條件保證了變換(1)將V'的內部變換成V中的內部,將V'的邊界變換成V的邊界。我們知道了V的邊界,也就知道了V'的邊界,反之亦然。
在三重積分中有兩個常用的變換。
柱面坐標變換
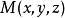 三重積分換元法
三重積分換元法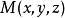 三重積分換元法
三重積分換元法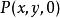 三重積分換元法
三重積分換元法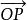 三重積分換元法
三重積分換元法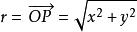 三重積分換元法
三重積分換元法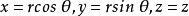 三重積分換元法
三重積分換元法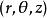 三重積分換元法
三重積分換元法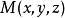 三重積分換元法
三重積分換元法任取xyz空間中的一點 。設點 在xy平面上的投影為點 ,連線O,P兩點,得到向量 , ,則有 , 稱為點 的柱面坐標,於是我們得到柱面坐標變換:
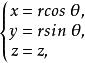 三重積分換元法
三重積分換元法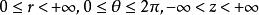 三重積分換元法
三重積分換元法其中 ,有
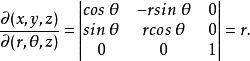 三重積分換元法
三重積分換元法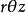 三重積分換元法
三重積分換元法柱面坐標變換並非一對一的,例如 空間一條直線段
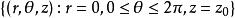 三重積分換元法
三重積分換元法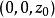 三重積分換元法
三重積分換元法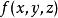 三重積分換元法
三重積分換元法對應於xyz空間中的一點 。與平面上極坐標變換類似,若函式 在有界閉體V上連續,可以證明
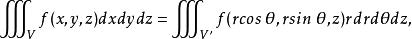 三重積分換元法
三重積分換元法其中V'是V在柱面坐標變換下的原象。
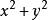 三重積分換元法
三重積分換元法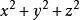 三重積分換元法
三重積分換元法當圍成體V的曲面的函式或被積函式含有“ ”或“ ”時,可考慮套用柱面坐標變換。
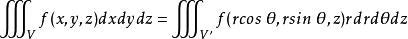 三重積分換元法
三重積分換元法可按下列步驟把 化成累次積分:
(1)在xyz空間中畫出V的草圖;
(2)把V朝xy平面投影,得到V在xy平面的投影區域D;
(3)把D用極坐標表示出來:
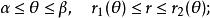 三重積分換元法
三重積分換元法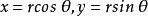 三重積分換元法
三重積分換元法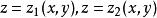 三重積分換元法
三重積分換元法(4)用 代入到V的上、下兩個曲面方程 中得到:
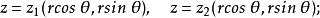 三重積分換元法
三重積分換元法(5)用聯立不等式表示V‘:
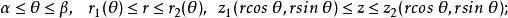 三重積分換元法
三重積分換元法(6)定限
 三重積分換元法
三重積分換元法球面坐標變換
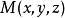 三重積分換元法
三重積分換元法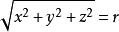 三重積分換元法
三重積分換元法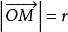 三重積分換元法
三重積分換元法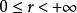 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法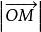 三重積分換元法
三重積分換元法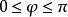 三重積分換元法
三重積分換元法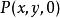 三重積分換元法
三重積分換元法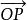 三重積分換元法
三重積分換元法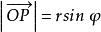 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法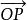 三重積分換元法
三重積分換元法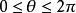 三重積分換元法
三重積分換元法任取xyz中的一點 ,令 ,有 , ;令 為 與z軸的正向夾角,則 。設點M在xy平面的投影為點 ,得 , ;令 為 與x軸的正向夾角,則 。於是
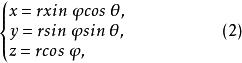 三重積分換元法
三重積分換元法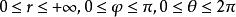 三重積分換元法
三重積分換元法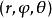 三重積分換元法
三重積分換元法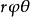 三重積分換元法
三重積分換元法其中 ,把 稱為點M的球面坐標,把式(2)看成從 空間到xyz空間的變換,有
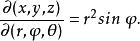 三重積分換元法
三重積分換元法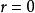 三重積分換元法
三重積分換元法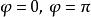 三重積分換元法
三重積分換元法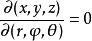 三重積分換元法
三重積分換元法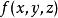 三重積分換元法
三重積分換元法球面坐標變換(2)並不是一對一的,並且當 或 時, 。若 在有界閉體V上連續,則有下面的公式成立 :
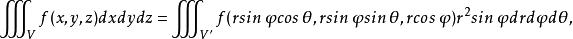 三重積分換元法
三重積分換元法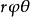 三重積分換元法
三重積分換元法其中V'是V在球面坐標變換(2)下所對應的 空間中的有界閉體。
在球面坐標中,
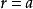 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法( 為常數),對應於原點為中心,以 為半徑的球面;
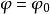 三重積分換元法
三重積分換元法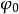 三重積分換元法
三重積分換元法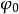 三重積分換元法
三重積分換元法( 為常數),對應於以原點為頂點,z軸為中心軸,半頂角為 的圓錐面;
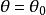 三重積分換元法
三重積分換元法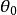 三重積分換元法
三重積分換元法( 為常數),對應於以z軸為邊緣的半平面。
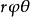 三重積分換元法
三重積分換元法設V'是V在球面坐標變換(2)所對應的空間中的立體。把
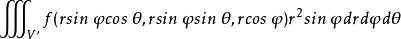 三重積分換元法
三重積分換元法化成累次積分的步驟如下:
(1)畫出V的草圖;
 三重積分換元法
三重積分換元法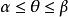 三重積分換元法
三重積分換元法(2)把立體V投影到xyz平面上,得到投影區域D,看的變化範圍:;
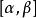 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法(3)在中任意取定一個,得到半平面,從半平面與V表面的截線看的變化範圍:
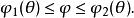 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法 三重積分換元法
三重積分換元法(4)取定以上的與,得到位於V中的半平面與錐面的交線段,從交線段看r的變化範圍:
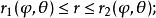 三重積分換元法
三重積分換元法於是
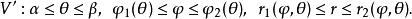 三重積分換元法
三重積分換元法則
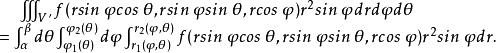 三重積分換元法
三重積分換元法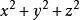 三重積分換元法
三重積分換元法球面坐標變換一般用在積分區域為球體或圓錐體或被積函式含有因子的三重積分的計算中。
