概念
插值是離散函式逼近的重要方法,利用它可通過函式在有限個點處的取值狀況,估算出函式在其他點處的近似值。常用的插值方法有多項式插值、樣條差值、分段插值、三角插值等。
而 三角插值,作為常用的插值方法之一,是指取插值函式為三角多項式的插值方法。特別適用於對周期函式的插值.設被插值函式f(x)為以2二為周期的函式,取n階三角多項式稱上式為 高斯三角插值公式 。
相關定理
定理1
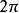 三角插值
三角插值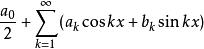 三角插值
三角插值設函式f的周期函式為 、且具有連續的一階導數,則Fourier級數 一致收斂於f。其中係數有下列公式計算:
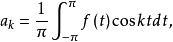 三角插值
三角插值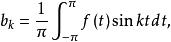 三角插值
三角插值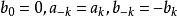 三角插值
三角插值顯然係數滿足 。
定理2
Flourier級數定理)
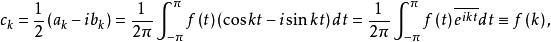 三角插值
三角插值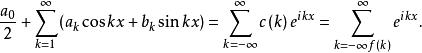 三角插值
三角插值設,則
三角多項式
在數學中, 三角多項式是一類基於三角函式的函式的總稱。三角多項式是可以表示成有限個正弦函式sin( nx) 和餘弦函式cos( nx) 的和的函式,其中的 x是變數,而 n是一個自然數。三角多項式中每一項的係數可以是實數或者複數。如果係數是複數的話,那么這個三角多項式是一個傅立葉級數。
三角多項式在許多數學分支,如數學分析和數值分析中都有套用,例如在傅立葉分析中,三角多項式被用於傅立葉級數的表示,在三角插值法中,三角多項式被用於逼近周期性函式 。
定義
一個函式 T如果能夠寫成:
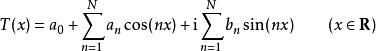 三角插值
三角插值 三角插值
三角插值的形式,其中對於所有的 , a和 b都是複數,那么就稱其為 N階復三角多項式。運用歐拉公式,這個函式可以寫為:
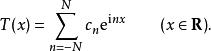 三角插值
三角插值同樣地,如果對於所有的{\displaystyle 0\leq n\leq N}, a和 b都是實數的話,那么函式 t
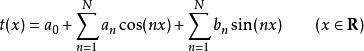 三角插值
三角插值就被稱 N階實三角多項式。
性質
 三角插值
三角插值 三角插值
三角插值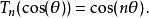 三角插值
三角插值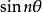 三角插值
三角插值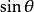 三角插值
三角插值 三角插值
三角插值是關於的 n次多項式, 實際上,這種多項式稱為第一類切比雪夫多項式。同樣地, 也是關於 和 的 n次多項式,稱為第二類切比雪夫多項式。
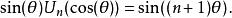 三角插值
三角插值 三角插值
三角插值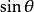 三角插值
三角插值因此,一個三角多項式實際上也可以認為是關於三角函式 和 的多項式。
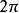 三角插值
三角插值三角多項式都是周期為 的周期函式。同時,任何連續的周期函式都可以藉助於三角多項逼近到任意接近的程度。
套用
( 費耶三角插值)在傅利葉譜分析中 ,一旦函式 f 的狄利克雷和係數通過在等距節點處的數值求積確定下來 ,結果函式就在這些點處插值 f 並以高精度逼近連續部分和 。 通過研究三角多項式和立方樣條差值逼近連續費耶和問題 ,可以得到以下結果 :連續費耶和可以通過兩個費耶插值的平均以高精度逼近 ,一個在偶指標結點集插值 f ,另一個在奇指標結點集插值 f ,由於立方樣條插值容易構造 ,所以它常被用來代替 三角插值 。
傅立葉和並不對所有連續函式收斂 ,而費耶和對所有連續函式都收斂 , 三角插值理論的幾個過程都可以通過費耶和的方式得到 ,大多數情況下這些多項式的一致收斂性也可以通過對應的多項式顯示形式直接得到 。由可和函式的費耶定理可以得到一個重要事實 ,即 :所有可和函式均由其傅立葉係數唯一確定 。
許多人研究過三角插值求和表明 ,在許多情況下 ,傅利葉級數的每個收斂或可和性理論 ,都可以移植到等距節點的三角插值過程的收斂性或可和性 ,這一類型的運算元可看作離散運算元的特例 。
