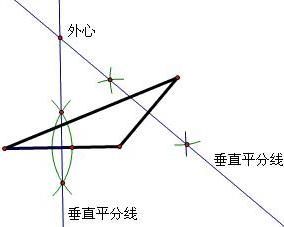
基本定義
三角形外接圓的圓心叫做三角形的外心．
三角形外接圓的圓心也就是三角形三邊垂直平分線的交點,三角形的三個頂點就在這個外接圓上
共點證明
.
∵l、m分別為線段AB、AC的中垂線
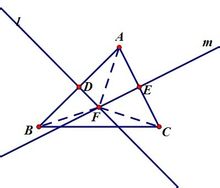三角形外心∴AF=BF=CF
∴BC中垂線必過點F
性質
設⊿ABC的外接圓為☉G(R)，角A、B、C的對邊分別為a、b、c，p=(a+b+c)/2．
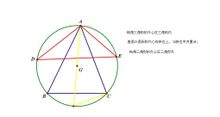三角形外心性質1：（1）銳角三角形的外心在三角形內；
（2）直角三角形的外心在斜邊上，與斜邊中點重合；
（3）鈍角三角形的外心在三角形外.
（4）等邊三角形外心與內心為同一點。
性質2：∠BGC=2∠A，（或∠BGC=2(180°-∠A)）.
性質3：∠GAC+∠B=90°
證明：如圖所示延長AG與圓交與P（B、C下面的那個點）
∵A、C、B、P四點共圓
∴∠P=∠B
∵∠P+∠GAC=90°
∴∠GAC+∠B=90°
性質4：點G是平面ABC上一點，點P是平面ABC上任意一點，那么點G是⊿ABC外心的充要條件是：
（1）向量PG=(tanB+tanC)向量PA+(tanC+tanA)向量PB+(tanA+tanB)向量PC)/2(tanA+tanB+tanC).
或（2）向量PG=(cosA/2sinBsinC)向量PA+(cosB/2sinCsinA)向量PB+(cosC/2sinAsinB)向量PC.
性質5：三角形三條邊的垂直平分線交於一點，該點即為三角形外接圓的圓心.外心到三頂點的距離相等。
性質6：點G是平面ABC上一點，那么點G是⊿ABC外心的充要條件(向量GA+向量GB)·向量AB= (向量GB+向量GC)·向量BC=(向量GC+向量GA)·向量CA=0.
做法
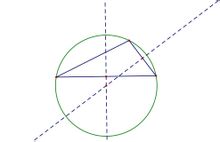三角形外心分別作三角形兩邊的中垂線交點計作O
以O為圓心OA為半徑畫圓
圓O即為所求
