基本介紹
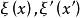 一維射影對應
一維射影對應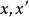 一維射影對應
一維射影對應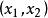 一維射影對應
一維射影對應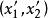 一維射影對應
一維射影對應設有點列 , 關於各自的一維射影坐標系的坐標分別為 及 ,則滿足
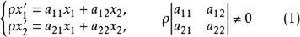 一維射影對應
一維射影對應 一維射影對應
一維射影對應 一維射影對應
一維射影對應 一維射影對應
一維射影對應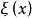 一維射影對應
一維射影對應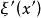 一維射影對應
一維射影對應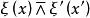 一維射影對應
一維射影對應由點列 到 的一一映射 ,叫做由 到 的射影對應,記作 。
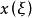 一維射影對應
一維射影對應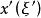 一維射影對應
一維射影對應對偶地,可以定義線束 到 的射影對應。兩點列間和兩線束間的射影對應統稱為一維射影對應,
顯然,一維射影對應(1)的逆對應也是一維射影對應。
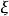 一維射影對應
一維射影對應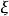 一維射影對應
一維射影對應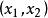 一維射影對應
一維射影對應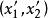 一維射影對應
一維射影對應特別地,稱直線 到自身的射影對應為直線 上的射影變換,這時(1)中 與 認為是任一對對應點關於同一坐標系的坐標。
只要適當選擇坐標系,一維射影對應式(1)可化為更簡單的形式。
相關定理及證明
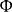 一維射影對應
一維射影對應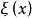 一維射影對應
一維射影對應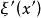 一維射影對應
一維射影對應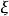 一維射影對應
一維射影對應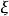 一維射影對應
一維射影對應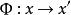 一維射影對應
一維射影對應定理1 設 為點列 到 的射影對應,則對於 上任意確定的射影坐標系,必存在 '上的一個射影坐標系,使得 了表示為
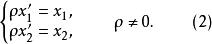 一維射影對應
一維射影對應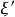 一維射影對應
一維射影對應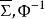 一維射影對應
一維射影對應證:設對於 上某個射影坐標系 可表示為
 一維射影對應
一維射影對應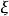 一維射影對應
一維射影對應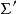 一維射影對應
一維射影對應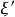 一維射影對應
一維射影對應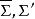 一維射影對應
一維射影對應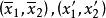 一維射影對應
一維射影對應由定理知在 '上必存在射影坐標系 ,使 上任一點x'在 下的坐標 之間滿足關係式
 一維射影對應
一維射影對應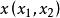 一維射影對應
一維射影對應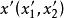 一維射影對應
一維射影對應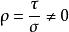 一維射影對應
一維射影對應由(1'),(2')知 與 間必滿足(2),其中 。
定理2 兩點列間的射影對應保持四點的交比不變(以下簡稱為“保交比”);反之,兩直線間保持交比不變的一一對應是射影對應。
推論 兩拓廣直線間的中心射影是射影對應。
定理3 兩點列間的射影對應由三對相異對應點唯一決定。
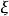 一維射影對應
一維射影對應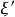 一維射影對應
一維射影對應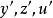 一維射影對應
一維射影對應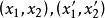 一維射影對應
一維射影對應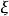 一維射影對應
一維射影對應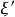 一維射影對應
一維射影對應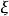 一維射影對應
一維射影對應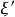 一維射影對應
一維射影對應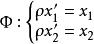 一維射影對應
一維射影對應證 設 上三相異點y,z,u分別對應 上三相異點 ;又設 分別是 和 上以y,z,u和y',z',u'為參考點的射影坐標,則 到 的射影對應 ,顯然使得y,z,u分別對應y',z',u',故存在性得證。
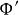 一維射影對應
一維射影對應另設射影對應 也使y,z,u分別對應y',z',u',把這三對對應點的坐標分別代入式(1)得
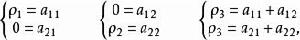 一維射影對應
一維射影對應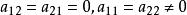 一維射影對應
一維射影對應於是 。
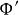 一維射影對應
一維射影對應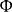 一維射影對應
一維射影對應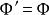 一維射影對應
一維射影對應從而 的表達式與 相同,故 ,唯一性得證。
推論 直線上的射影變換,若使三個點不變(即有三個固定點),則必為恆等變換。
附註一維射影對應式(3.1.1)的非齊次形式為
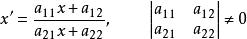 一維射影對應
一維射影對應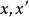 一維射影對應
一維射影對應也可寫成 的雙線性方程
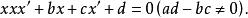 一維射影對應
一維射影對應一維射影對應的特徵性質是一一對應保交比,也可說成是一一對應保調和比,事實上有下述定理。
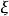 一維射影對應
一維射影對應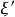 一維射影對應
一維射影對應定理4 一個把直線 上的點變為直線 上的點的一一對應,若把調和共軛的四個點變成調和共軛的四個點,則這個對應是射影對應,該定理稱達布(Darboux)定理。

