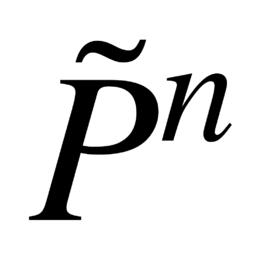簡介
射影對應亦稱射影映射(projective mapping)、直射映射(collineation mapping)。
 射影對應
射影對應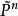 射影對應
射影對應射影空間 到射影空間 的映射F稱為射影映射:
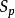 射影對應
射影對應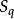 射影對應
射影對應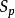 射影對應
射影對應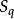 射影對應
射影對應(1)如果子空間 ⊂ ,則F( )⊂F( );
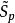 射影對應
射影對應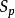 射影對應
射影對應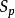 射影對應
射影對應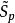 射影對應
射影對應(2)對於每個子空間 ,存在 ,使得F( )= ;
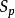 射影對應
射影對應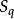 射影對應
射影對應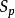 射影對應
射影對應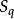 射影對應
射影對應(3) = ,若且唯若F( )=F( )。
一維射影映射
設 l和 l’是兩條射影直線, f是從 l上的點集到 l’上的1-1映射,保持 l上的任何四點的調和共軛性不變(即:若 l上的四點A,B,C和D滿足交比(AB,CD)=-1,則f(A)=A’,f(B)=B’,f(C)=C’和f(D)=D’滿足(A'B',C'D')=-1),則稱 f為從1到 I'的一維射影映射(onedimensional projective mapping)。
一維射影映射保持任何四點的交比不變,且其逆映射也是一維射影映射。
兩個一維射影映射的合成仍是一維射影映射。
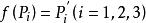 射影對應
射影對應一維射影映射由三對對應點唯一決定(一維射影映射的基本定理),即: 若P₁,P₂和P₃是 l上的三個不同點,P'₁,P'₂和P'₃是 l'上的三個不同點,則有唯一的射影映射 f,使 。
一條射影直線到自身的射影映射稱為一個一維射影變換。若一個一維射影變換有三個不同的不變點,則該一維射影變換是恆等變換。設 l上的點P的射影坐標為(x'₁,x'₂),點f(P)=P'的射影坐標為(x₁,x₂),則 f可以由下列非奇異線性變換來表示:
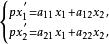 射影對應
射影對應 射影對應
射影對應 射影對應
射影對應其中一切 ∈ℝ為常數,且ρ≠0,係數行列式det( )≠0。
二維射影映射
設π和π'是兩個射影平面, f是從π上的點集到π'上的點集的1-1映射,保持點的共線性不變(即: π 上的共線點的象是π'上的共線點),則稱 f為從π到π'的二維射影映射(two-dimensional projective mapping)。
二維射影映射保持共線四點的交比不變,且其逆映射也是二維射影映射。
兩個二維射影映射的合成仍是二維射影映射。
二維射影映射由四對一般位置的對應點唯一決定(二維射影映射的基本定理),即:
若P₁,P₂,P₃和P₄是π上的四個不同點,其中任何三點不共線,P'₁,P'₂,P'₃和P'₄是π'上的四個不同點,其中任何三點也不共線,則有唯一的射影映射 f,使f(Pᵢ)= P'ᵢ(i= 1,2,3,4)。
一個射影平面到自身的射影映射稱為一個二維射影變換。若一個二維射影變換有四個不同的不變點,其中任何三個不共線,則該二維射影變換是恆等變換。
設π上的點P 的射影坐標為(x₁,x₂,x₃),點 f(P)=P'的射影坐標為(x'₁,x'₂,x'₃),則 f可以由下列非奇異線性變換來表示:
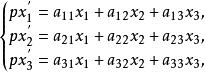 射影對應
射影對應 射影對應
射影對應 射影對應
射影對應其中一切 ∈ℝ為常數,且ρ≠0,係數行列式det( )≠0。
從π到π'的二維射影映射 f誘導出從π上的直線集到π'上的直線集的1-1映射 f',因為π上的任意直線 l上的點在 f下的象必在π'上的某直線 l'上,從而產生了映射 f' :l→I'。
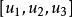 射影對應
射影對應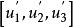 射影對應
射影對應設 l的直線坐標為 , I'的直線坐標為 ,則 f'也可以由非奇異線性變換來表示:
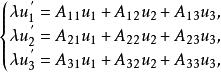 射影對應
射影對應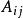 射影對應
射影對應 射影對應
射影對應 射影對應
射影對應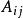 射影對應
射影對應其中λ≠0。 是 在det( ) 中的代數餘子式,係數行列式det( ) ≠0。
三維射影映射
設K 和K'是兩個射影空間, f是從K中的點集到K'中的點集的1-1映射,保持點的共面性不變(即: K 中的共麵點的像是K'中的共麵點),則稱 f為從K到K'的三維射影映射(three-dimensional project ive mapping)。
三維射影映射保持點的共線性和K中的任何共線四點的交比不變,且其逆映射也是三維射影映射。
兩個三維射影映射的合成仍是三維射影映射。
三維射影映射由五對一般位置的對應點唯一決定(三維射影映射的基本定理),即: 若P₁,P₂,P₃,P₄和P₅是K中的五個不同點,其中任何四點不共面,P'₁,P'₂,P'₃,P'₄和P'₅則有唯一的射影映射 f,使f(Pᵢ)= P'ᵢ(i= 1,2,3,4,5)。
一個射影空間到自身的射影映射稱為一個三維射影變換。
若一個三維射影變換有五個不同的不變點,其中任何四個不共面,則該三維射影變換是恆等變換。
設k中的點p的射影坐標為(x₁,x₂,x₃,x₄)點f(P)=P'的射影坐標為(x'₁,x'₂,x'₃,x'₄),則 f可以由下列非奇異線性變換來表示:
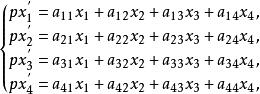 射影對應
射影對應 射影對應
射影對應 射影對應
射影對應其中一切 ∈ℝ為常數,且ρ≠0,係數行列式det( )≠0。
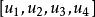 射影對應
射影對應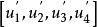 射影對應
射影對應從K到K'的三維射影映射 f誘導出從K中的平面集到K'中的平面集的1-1映射 f'。因為K中的任意平面α上的點在 f下的象必在K'上的某平面α'上,從面產生了映射f'≠α→α。設α的平面坐標為 ,α'的平面坐標為 ,則 f'也可以由非奇異線性變換來表示:
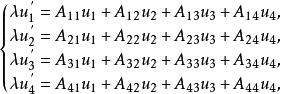 射影對應
射影對應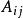 射影對應
射影對應 射影對應
射影對應 射影對應
射影對應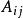 射影對應
射影對應其中λ≠0,是在det() 中的代數餘子式,係數行列式det() ≠0。