基本概念
在射影幾何中，所有幾何圖形都是由以下的基本形構成：
二維基本形 二維基本形定義1 屬於一條直線 的所有點A，B，C，……的集合，稱為以 為底的 點列。記作
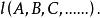二維基本形定義2 一個平面上經過一點P的所有直線a，b，c，……的集合，稱為以P為中心的 線束。記作
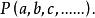二維基本形
二維基本形 二維基本形定義3 屬於一個平面 的所有直線A，B，C，……的集合，稱為以 為底的 點場。記作
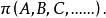二維基本形 二維基本形 二維基本形定義4 屬於一個平面 的所有直線a，b，c，……的集合，稱為以 為底的 線場。記作
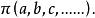二維基本形 二維基本形點列的點，線束的直線，其自由度均為1，故稱點列和線束為 一維基本形。同理，點場和線場稱為 二維基本形。也常把以 為底的點場和線場合稱為 點線場 。
二維射影變換
一維基本形的透視對應、射影對應，可推廣到二維基本形中，對點線場進行類似的討論。
其實若將點列、線束視為射影平面(二維射影空間)的子空間，則一維基本形的射影對應是平面到自身的元素間的對應，即二維的射影變換。
因此，二維射影變換是點線場的元素間的一一對應，且經變換四元素的交比不變。
其中將點變成點，直線變成直線的變換保同素性，稱為 同素變換或 直射變換，否則，稱為對射變換。
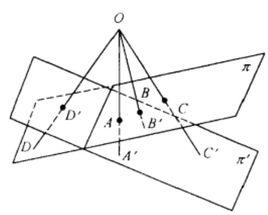
定義1 二平面的點之間的透視對應就是二平面之間點的一一對應，使得對應點的連線共點，如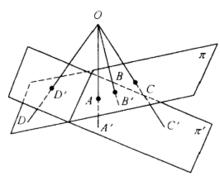圖1。
圖1定義2 兩個平面間的一一對應，如果滿足下列條件 ：
(1)保持點和直線的結合性；
(2)任何共線四點的交比等於其對應四點的交比，則此一一對應叫做 射影對應。
同樣可以給出兩個平面間的直線間的射影對應的定義。
兩個平面的點之間或直線之間的射影對應是 同素對應(點對應點從而直線對應直線，或直線對應直線從而點對應點)，通常我們只討論點到點間的同素對應，由射影對應定義可以看到以下性質：
(1)兩平麵點之間的透視對應必是射影對應。
(2)若干次透視對應(透視鏈)的結果必為射影對應。
(3)兩平面間的射影對應是一種等價關係。
定義3 在定義2中，如果兩對應平面是重合的，則所建立的射影對應叫做該平面的 射影變換。
我們所討論的射影對應和射影變換，一般都是同素的，簡稱為 同素變換 。
