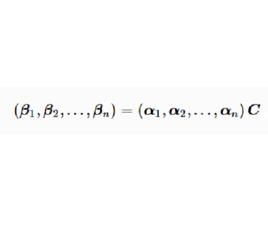基本知識
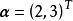 基變換
基變換 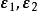 基變換
基變換 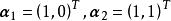 基變換
基變換 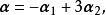 基變換
基變換 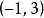 基變換
基變換 在向量空間中,任一向量在指定基下的坐標是唯一的,但在不同基下的坐標一般是不同的。例如在自然基下的坐標為(2,3),但在基下, 由於故在此基下的坐標為。
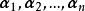 基變換
基變換 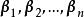 基變換
基變換 定義1 設向量組和是n維向量空間V的兩個基,若它們之間的關係可表示為
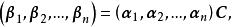 基變換
基變換 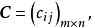 基變換
基變換 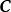 基變換
基變換 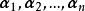 基變換
基變換 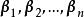 基變換
基變換 其中則稱矩陣為從基到基的 過渡矩 陣(或 基變換矩陣)。此式為 基變換公式.
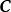 基變換
基變換 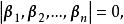 基變換
基變換 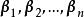 基變換
基變換 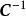 基變換
基變換 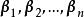 基變換
基變換 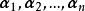 基變換
基變換 易知,是可逆矩陣,否則即不是n維向量空間V的基,另外,是從到基的過渡矩陣,即
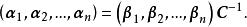 基變換
基變換 相關定理
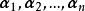 基變換
基變換 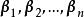 基變換
基變換 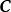 基變換
基變換 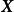 基變換
基變換 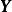 基變換
基變換 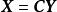 基變換
基變換 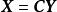 基變換
基變換 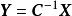 基變換
基變換 定理設向量空間V的一組基到另一組基的過渡矩陣為,V中一個向量在這兩組基下的坐標分別為和,則,我們也稱為坐標變換公式,同時也有.
例題分析
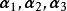 基變換
基變換 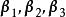 基變換
基變換 例1 設向量組和是 R 的兩個基,且有
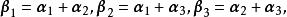 基變換
基變換 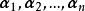 基變換
基變換 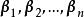 基變換
基變換 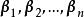 基變換
基變換 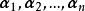 基變換
基變換 求從基到基的過渡矩陣和從基到基的過渡矩陣。
解: 由
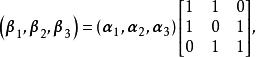 基變換
基變換 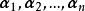 基變換
基變換 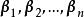 基變換
基變換 得從基到基的過渡矩陣為
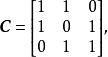 基變換
基變換 由
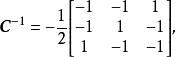 基變換
基變換 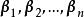 基變換
基變換 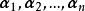 基變換
基變換 得從基到基的過渡矩陣為
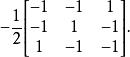 基變換
基變換