t道

粒子2到2散射過程，在量子場論中計算其費曼圖時，考慮到交叉對稱性，按照傳播子的四動量對樹圖進行分類；當傳播子的四動量是Mandelstam變數中的t時，我們稱這類圖為t道。

定義

假定入射粒子的動量為p、p'；出射粒子的動量為k、k'，如圖1所示 ：

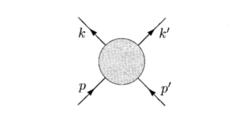圖1

我們不妨選取一個特例來進行說明：取入射粒子為一個費米子，一個反費米子；中間傳播一個標量粒子；出射粒子也是一個費米子，一個反費米子。這時費曼圖如圖2：

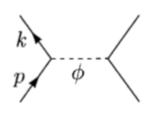圖2

t道

我們可以知道，中間傳播的場粒子的傳播子為：

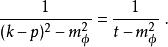t道

由此可以看出這一類圖的動量為t，故而稱這一類圖為t道的圖。

Mandelstam變數

t道

對於一個22的散射過程，我們可以設其入射粒子四動量分別為p、p' ；出射粒子四動量為k、k'。如圖1所示。我們定義Mandelstam變數為 ：

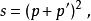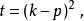t道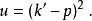

t道

t道

其中s、t、u就是我們定義的Mandelstam變數，其間運用了四動量的守恆定律。

套用

一般出末態粒子相同時（彈性散射），會有u道圖的貢獻，例如穆勒散射、Bhabha散射 。