radon變換

數學上，是一種積分變換，這個變換將二維平面函式變換成一個定義在二維空間上的一個線性函式(的意思是對做radon變換)，而 的值為函式對該條線做積分的值。以概述圖(左圖)為例，黃色區域即是，線則是代表。 radon變換是在公元1917年提出，他也同時提出radon變換的反變換公式，以及三次空間的radon變換公式。 而在不久之後，更高維度的歐幾里得空間的radon變換被提出。 在複數上有和radon變換相似的penrose變換，radon變換被廣泛的套用在斷層掃描，radon反變換可以從斷層掃描的剖面圖重建出投影前的函式 。

基本信息

• 中文名：radon變換
• 其他外文名：Radon transform
• 定義：是一種積分變換

• 對 應：原始函式的某個線積分值
• 含 有：直線成分
• 按 照：合適的角度

簡介

若函式F表示一個未知的密度，對F做radon變換，相當於得到F投影后的訊號，舉例來說：F相當於人體組織，斷層掃描的輸出訊號相當於經過radon變換的F。 因此，可以用radon反變換從投影后的密度函式，重建原始的密度函式，它也是重建斷層掃描的數學理論基礎，另一個被廣為人知名詞的是三維重建 。

radon變換後的訊號稱作“正弦圖”，因為一個偏離中心的點的radon變換是一個正弦曲線。所以對一些小點的radon變換，會看起來像很多不同振福、相位的正弦函式重疊在一起。

定義

令密度函式f(X)=f(x,y)是一個的定義域為R 的緊緻台(compact support)。令 R為radon變換的運運算元，則 Rf(x,y)是一個定義在R 空間中的直線L，它的定義如下 ：

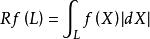radon變換

套用

radon變換可以套用在：X射線電腦斷層掃描、條碼掃描器、蛋白質複合體，而且也是雙曲線偏微分方程的解。