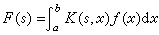積分變換
正文
通過參變數積分將一個已知函式變為另一個函式。已知ƒ(x),如果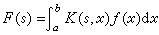
積分變換無論在數學理論或其套用中都是一種非常有用的工具。最重要的積分變換有傅立葉變換、拉普拉斯變換。由於不同套用的需要,還有其他一些積分變換,其中套用較為廣泛的有梅林變換和漢克爾變換,它們都可通過傅立葉變換或拉普拉斯交換轉化而來。
梅林變換 當K(s,x)=xs_1,x>0,而ƒ(x)定義於【0,+∞),函式
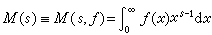 (1)
(1)
 (x>0), (2)
(x>0), (2)
(1)式與(2)式在一定條件下互為反演公式。例如,設(1)絕對收斂,在任何有限區間上 ƒ(x)是有界變差的,且已規範化:
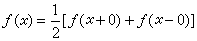 ,則由(1)可推得(2),在l2(0,∞)空間中也有類似結果。
,則由(1)可推得(2),在l2(0,∞)空間中也有類似結果。 若以M(s,ƒ′)表示ƒ′(x)的梅林變換, 則在一定條件下,有
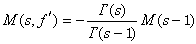 。在一定條件下,還有下列梅林交換的卷積公式:
。在一定條件下,還有下列梅林交換的卷積公式: 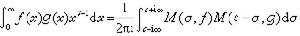 ,
,
一些簡單函式的梅林變換(α >0)如表:
 積分變換
積分變換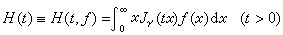 (3)
(3)
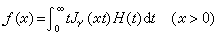 (4)
(4)

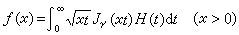 ,
,
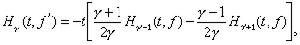
 積分變換
積分變換A.Erdélyi, ed.,table of Integral Transforms,Vol. 1, McGraw-Hill, New York, 1954.
特蘭台爾著,潘德惠譯:《數學物理中的積分變換》,高等教育出版社,北京,1959。(C.J.Tranter,Integral Transforms in MatheMatical Physics,2nd ed.,John Wiley & Sons, New York, 1956.)
D.V.Widder,An Introduction to Transform Theory,Academic Press, New York, 1972.