簡介
n線性運算元
n線性運算元是對n格變元分別是線性的運算元。
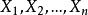n線性型設 與 Y 是賦范線性空間，
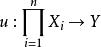n線性型
n線性型
n線性型若 分別對每一個變元 都是線性的，則稱 u 是n線性運算元。
定義
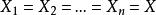n線性型
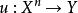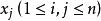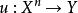n線性型 n線性型
n線性型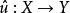 n線性型
n線性型設 ，如果 n 線性運算元 的值 在任意對調x 與 時不變，則稱u為對稱的n 線性運算元，對於 n 線性運算元 ，令 為
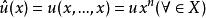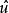n線性型
n線性型則 稱為u所對應的n次型。
n 次型亦稱n線性型。
性質
不同的 n 線性運算元可對應於相同的 n 次型。
對稱的n線性運算元與n次型之間一一對應。
線性型
線性型又稱線性函式或線性齊次，是域F上的線性空間V到域F上的一個線性映射。
如果f是從V到F的映射，對V的向量 x，y，F的元素a，b滿足f(a x+b y)=af( x)+bf( y),那么f就稱為V上的線性型或線性映射。
若 e, e,..., e是V的一組基，則V的每一個向量x都可以表示成x=x e+x e+…+x e，式中x在F域中，i=1,2,…,n。因此對於V上的線性型f有f( x)=xf( e)+xf( e)+…+xf( e)或記成f(x,x,…,x)=ax+ax+…+ax，式中f( e)=a，i=1,2,…,n。
