詳細介紹
特殊正交群是一類元素行列式為1的重要的典型群。正交群O(K,Q)的元素的行列式都是1或-1,其中行列式為1的全體正交變換組成一個子群,稱為特殊正交群,記為SO(K,Q)。當K的特徵≠2時,
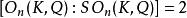 特殊正交群
特殊正交群此時SO(K,Q)也稱為旋轉群,並記為O(K,Q)。它也就是由偶數個對稱的乘積的全體組成的群。實正交群O(n)的旋轉群記為SO(n)或O。當K的特徵=2時,SO(K,Q)=O(K,Q)。設Q無虧數,即:
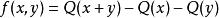 特殊正交群
特殊正交群是Q所定義的空間V上的非退化交錯型,n=2m為偶數,O(K,Q)<Sp(K,f)。取V的基e,e,…,e使f(e,e)=1(當j=i±m)或0(當j≠i±m)。對任一A∈Sp(K,f),若:
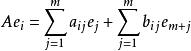 特殊正交群
特殊正交群則:
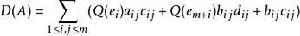 特殊正交群
特殊正交群稱為A的迪克森不變數。當A∈O(K,Q)時D(A)=0或1,滿足條件D(A)=0的全體正交變換A組成O(K,Q)的一個指數為2的子群,稱為旋轉群,記為O(K,Q).除n=4,K=F且Q的指數為2的情形外,旋轉群O(K,Q)就是O(K,Q)中偶數個正交平延的乘積的全體組成的子群。
群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。
子群
如果群G的非空子集合H對於G的運算也成一個群,那么H稱為G的子群。
子群是群的特殊的非空子集。群G的非空子集H,若對G的乘法也成為群,則稱H為G的子群,記為H≤G。若子群H≠G,則稱H為G的真子群,記為HG或簡記為H<G。任何一個非單位元群G至少有兩個子群,G自身以及由單位元e作成的單位元群{e}(或用{1}或1表示),稱它們為G的平凡子群。不是平凡子群的子群稱為非平凡子群。群G的非空子集H為G的子群的充分必要條件是:對任意的a,b∈H,恆有ab∈H。若{H|i∈I}是G的子群的集合,I是一個指標集,則所有H的交H是G的一個子群。
典型群
典型群是一類重要的群。一般線性群、酉群、辛群、正交群,以及它們的換位子群、對中心的商群等統稱為典型群。實數域和複數域上的典型群是李群的重要例子,它們的構造及表示在李群理論、幾何學、多複變函數論以至物理學中都起著重要作用。迪克森(Dickson,L.E.)通過對有限域上典型群的構造的研究得到了一大批有限單群。這是繼交錯群之後人們發現的又一批重要的有限單群系列。經過謝瓦萊(Chevalley,C.)的工作進一步擴展為有限李型單群的系列後,為有限單群分類的最後完成奠定了一個重要基礎。迪厄多內(Dieudonné,J.)將迪克森的工作加以推廣,通過研究任意體上的典型群的構造也得到了大量的單群。迪厄多內、施賴埃爾(Schreier,O.)、范·德·瓦爾登(Van der Waerden,B.L.)、華羅庚、萬哲先等對研究典型群的構造、自同構及同構作出了重要貢獻。
相關群
一般線性群
一般線性群亦稱全線性群。一類重要的典型群。若V是體K上n維右線性空間,則V上全體可逆線性變換在映射的乘法下構成一個群,稱為V上的一般線性群或全線性群,記為GL(V).體K上全體n×n可逆方陣在矩陣乘法下構成一個群,稱為K上n次一般線性群,記為GL(K)或GL(n,K)。取定V在K上任一組基後可將每個g∈GL(V)對應一個矩陣A∈GL(K),從而得到GL(V)到GL(K)上的一個同構。在這個意義下,可以將GL(V)與GL(K)等同起來。
酉群
酉群是一類重要的典型群。在複數域的特殊情形,全體n×n酉方陣在矩陣乘法下構成的群稱為n次酉群,記為U(n)。一般地,設K是帶有對合J:a→a-的體,V是K上n維列向量空間,f(x,y)=x-Hy是V上非退化厄米特型或反厄米特型,這裡H∈GL(K)且=εH,ε=±1。若A∈GL(V)使f(Ax,Ay)=f(x,y)對所有的x,y∈V成立,則稱A是關於f的酉變換。關於f的全體酉變換組成GL(V)的一個子群,稱為關於f的酉群,記為U(K,f).從矩陣的觀點看,U(K,f)={A∈GL(K)|HA=H}.當f是交錯雙線性型時U(K,f)就是辛群Sp(K,f);當K的特徵≠2且f是對稱雙線性型時U(K,f)就是正交群O(K,f);當K是複數域,J是復共軛,H=I時,酉群U(K,f)就是酉群U(n)。
辛群
辛群是一類重要的群。辛空間的自同構群。設(V,ω)是一辛空間,若φ:V→V是線性同構且滿足ω(φX,φY)=ω(X,Y),X,Y∈V,則稱φ為(V,ω)的一個自同構。(V,ω)的自同構全體構成群GL(V)的一個子群,記為SP(V,ω)。特別地,標準辛空間(K,ω)的自同構群記為Sp(2n,K)。若K=R(實數域),則把Sp(2n,K)簡記為Sp(2n)並稱它為2n維辛群。
正交群
正交群是一類重要的典型群。在實數域的特殊情形,全體n×n正交方陣在矩陣乘法下構成的群稱為n次正交群,記為O(n)。一般地,設V是域K上n維列向量空間,Q(x)=xAx是V上的非退化二次型(A是K上某個n×n矩陣),若g∈GL(V)使Q(gx)=Q(x)對所有的x∈V成立,則稱g是關於Q的正交變換。關於Q的全體正交變換在映射乘法下構成一個群,稱為關於Q的正交群,記為O(K,Q)。當K的特徵≠2時,V上每個非退化對稱雙線性型f也決定一個正交群:
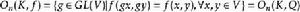 特殊正交群
特殊正交群其中Q(x)=f(x,x)/2。當K是實數域,Q是單位二次型Q(x)=x·x時的正交群O(K,Q)就是O(n)。
