定義
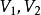 雙線性型
雙線性型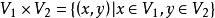 雙線性型
雙線性型設 都是域 K 上的向量空間,f 是直積 到 K 的映射。如果 f 滿足
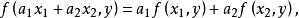 雙線性型
雙線性型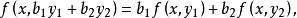 雙線性型
雙線性型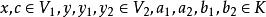 雙線性型
雙線性型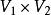 雙線性型
雙線性型其中 ,則稱 f 是由 到 K 的雙線性型或雙線性函式 (bilinear function)。
性質
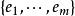 雙線性型
雙線性型 雙線性型
雙線性型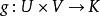 雙線性型
雙線性型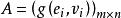 雙線性型
雙線性型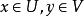 雙線性型
雙線性型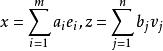 雙線性型
雙線性型設U,V分別是數域K上m維和n維線性空間, 與 分別是U與V的基, 是雙線性型。令 ,若 ,設 ,則
 雙線性型
雙線性型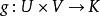 雙線性型
雙線性型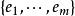 雙線性型
雙線性型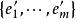 雙線性型
雙線性型 雙線性型
雙線性型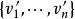 雙線性型
雙線性型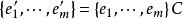 雙線性型
雙線性型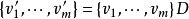 雙線性型
雙線性型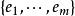 雙線性型
雙線性型 雙線性型
雙線性型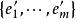 雙線性型
雙線性型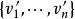 雙線性型
雙線性型設 是雙線性型, 與 是U的基, 與 是V的基,且 , ,設g在基 與 下矩陣為A,在 與 下矩陣為B,則B=C'AD。因此,g在不同基下的表示矩陣是相抵的,矩陣A的秩稱為g的秩。
定理
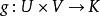 雙線性型
雙線性型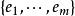 雙線性型
雙線性型 雙線性型
雙線性型設是雙線性型,則存在U的基與V的基,使得
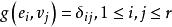 雙線性型
雙線性型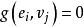 雙線性型
雙線性型其中,r=秩(g)。
非退化雙線性型
設f是線性空間V上的雙線性函式,如果它在某組基下的度量矩陣A是可逆矩陣,則稱f是非退化的雙線性函式,否則稱為退化的雙線性函式。

